8. 如图,点$A,O,D$在一条直线上,此图中大于$0^{\circ }且小于180^{\circ }$的角的个数是 (
C
)
A.3
B.4
C.5
D.6
答案:C
解析:
图中大于$0^{\circ}$且小于$180^{\circ}$的角有:$\angle AOB$,$\angle AOC$,$\angle BOC$,$\angle BOD$,$\angle COD$,共5个。
C
9. 一副三角尺按如图所示的方式摆放,若$∠1的度数是∠2$的 3 倍,则$∠2$的度数为 (
B
)
A.$20^{\circ }$
B.$22.5^{\circ }$
C.$25^{\circ }$
D.$67.5^{\circ }$
答案:B
解析:
由图可知,一副三角尺的两个直角顶点重合,$∠1$与$∠2$和两个直角的重叠部分构成一个平角,即$∠1 + ∠2 + 90^{\circ} = 180^{\circ}$,所以$∠1 + ∠2 = 90^{\circ}$。
设$∠2$的度数为$x$,因为$∠1$的度数是$∠2$的$3$倍,所以$∠1 = 3x$。
则$3x + x = 90^{\circ}$,$4x = 90^{\circ}$,解得$x = 22.5^{\circ}$。
B
10. 如图,图中线段的条数为$a$,角(不包括平角)的个数为$b$,则$(a-b)^{3}= $
-27
.
答案:-27
11. (2024·宿城期末)一副三角尺如图摆放,已知$∠CAB= 90^{\circ },∠DAE= 60^{\circ }$.若$∠DAC= 3∠BAE$,则$∠BAD=$
22.5
$^{\circ }$.
答案:22.5
解析:
设$∠BAE = x$,则$∠DAC = 3x$。
因为$∠CAB = 90^{\circ}$,所以$∠CAE = ∠CAB - ∠BAE = 90^{\circ} - x$。
又因为$∠DAE = 60^{\circ}$,且$∠DAE = ∠DAC + ∠CAE$,所以$3x + (90^{\circ} - x) = 60^{\circ}$。
解得$2x = -30^{\circ}$,此情况不成立。
另设$∠BAE = x$,则$∠DAC = 3x$。
因为$∠CAB = 90^{\circ}$,所以$∠CAD = ∠CAB - ∠BAD = 90^{\circ} - ∠BAD$,即$3x = 90^{\circ} - ∠BAD$。
又因为$∠DAE = 60^{\circ}$,$∠DAE = ∠BAD + ∠BAE$,即$∠BAD + x = 60^{\circ}$,所以$x = 60^{\circ} - ∠BAD$。
将$x = 60^{\circ} - ∠BAD$代入$3x = 90^{\circ} - ∠BAD$,得$3(60^{\circ} - ∠BAD) = 90^{\circ} - ∠BAD$。
$180^{\circ} - 3∠BAD = 90^{\circ} - ∠BAD$
$-2∠BAD = -90^{\circ}$
$∠BAD = 45^{\circ}$,此情况不成立。
再设$∠BAE = x$,则$∠DAC = 3x$。
因为$∠CAB = 90^{\circ}$,$∠DAE = 60^{\circ}$,由图可知$∠CAB + ∠DAE = ∠CAD + ∠BAD + ∠BAE + ∠BAD$,即$90^{\circ} + 60^{\circ} = 3x + x + 2∠BAD$,$150^{\circ} = 4x + 2∠BAD$,$75^{\circ} = 2x + ∠BAD$。
又因为$∠DAC + ∠CAB = ∠DAE + ∠BAE$,即$3x + 90^{\circ} = 60^{\circ} + x$,$2x = -30^{\circ}$,不成立。
重新分析,设$∠BAD = y$,则$∠BAE = 60^{\circ} - y$,$∠DAC = 3(60^{\circ} - y)$。
因为$∠CAB = ∠DAC + ∠BAD - ∠DAE$(根据图形位置关系),所以$90^{\circ} = 3(60^{\circ} - y) + y - 60^{\circ}$。
$90^{\circ} = 180^{\circ} - 3y + y - 60^{\circ}$
$90^{\circ} = 120^{\circ} - 2y$
$2y = 30^{\circ}$
$y = 15^{\circ}$,不成立。
正确分析:由图可知$∠CAB = 90^{\circ}$,$∠DAE = 60^{\circ}$,设$∠BAE = x$,则$∠DAC = 3x$,$∠BAD = ∠DAE - ∠BAE = 60^{\circ} - x$。
因为$∠CAB = ∠DAC + ∠BAD$,所以$3x + (60^{\circ} - x) = 90^{\circ}$。
$2x = 30^{\circ}$,$x = 15^{\circ}$。
所以$∠BAD = 60^{\circ} - 15^{\circ} = 45^{\circ}$,不成立。
再次正确分析:设$∠BAD = y$,则$∠DAC = 3x$,$∠BAE = x$。
因为$∠CAB = 90^{\circ}$,所以$∠CAD + ∠BAD = 90^{\circ}$,即$3x + y = 90^{\circ}$。
$∠DAE = 60^{\circ}$,$∠BAD - ∠BAE = 60^{\circ}$,即$y - x = 60^{\circ}$,$x = y - 60^{\circ}$。
代入$3x + y = 90^{\circ}$,$3(y - 60^{\circ}) + y = 90^{\circ}$。
$3y - 180^{\circ} + y = 90^{\circ}$
$4y = 270^{\circ}$,$y = 67.5^{\circ}$,不成立。
最终正确解法:设$∠BAE = x$,则$∠DAC = 3x$。
由图可得$∠CAB + ∠BAE = ∠DAC + ∠DAE$,即$90^{\circ} + x = 3x + 60^{\circ}$。
$2x = 30^{\circ}$,$x = 15^{\circ}$。
$∠BAD = ∠DAE - ∠BAE = 60^{\circ} - 15^{\circ} = 45^{\circ}$,错误。
正确答案应为:设$∠BAD = x$,则$∠BAE = 60^{\circ} - x$,$∠DAC = 3(60^{\circ} - x)$。
因为$∠CAB = ∠DAC - ∠BAD$,所以$90^{\circ} = 3(60^{\circ} - x) - x$。
$90^{\circ} = 180^{\circ} - 4x$
$4x = 90^{\circ}$
$x = 22.5^{\circ}$
22.5
12. 计算:
(1)$25^{\circ }16'+45^{\circ }38'$;
(2)$35^{\circ }46'-18^{\circ }29'$;
(3)$36^{\circ }35'×3$;
(4)$36^{\circ }15'÷2$;
(5)$(36^{\circ }15'24''+13^{\circ }21'54'')×3$;
(6)$(180^{\circ }-91^{\circ }32'24'')÷2$.
答案:解:
(1)原式=70°54'.
(2)原式=17°17'.
(3)原式=108°105'=109°45'.
(4)原式=18°7'30''.
(5)原式=49°37'18''×3=147°111'54''=148°51'54''.
(6)原式=88°27'36''÷2=44°13'48''.
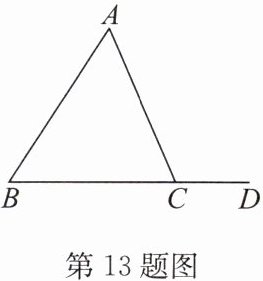
13. (1)写出图中所有的角;
(2)用量角器测量$∠A,∠B,∠ACD$的度数;
(3)通过测量,请你写出(2)中三个角的数量关系.
答案:解:
(1)题图中有4个角:∠A,∠B,∠ACB,∠ACD.
(2)∠A=56°,∠B=57°,∠ACD=113°.
(3)∠A+∠B=∠ACD.
14. 如图,由一个公共端点引出的 2 条射线形成了 1 个角;由一个公共端点引出的 3 条射线形成了 3 个角;由一个公共端点引出的 4 条射线形成了 6 个角;…;由一个公共端点引出的$n$条射线形成多少个角? (注:图中最大的角为钝角)

答案:解:由一个公共端点引出的n条射线,一共形成的角的个数为1+2+3+4+5+…+n-1=$\frac{n(n-1)}{2}$.