1. 三边
分别相等
的两个三角形全等(可以简写成
边边边
或
SSS
).
答案:分别相等 边边边 SSS
如图,在$\triangle ABC和\triangle DEF$中,
DE
=
AC
,
DF
=
BC
,∴$\triangle ABC\cong \triangle DEF$(
SSS
).
答案:DE AC DF BC SSS
解析:
在$\triangle ABC$和$\triangle DEF$中,
$\left\{\begin{array}{l} AB=DE\\ AC=DF\\ BC=EF\end{array}\right.$
$\therefore \triangle ABC\cong \triangle DEF(SSS)$
1. 如图是一个平分角的仪器,其中$AB= AD$,$BC= DC$.将点$A$放在一个角的顶点,$AB和AD$沿着这个角的两边放下,利用全等三角形的性质就能说明射线$AC$是这个角的平分线,这里判定$\triangle ABC和\triangle ADC$是全等三角形的依据是
SSS
.
答案:SSS
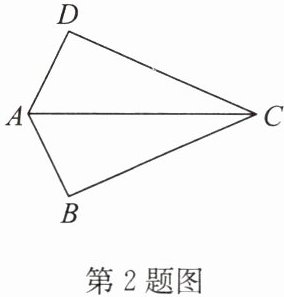
2. 如图,$AB= AD$,$BC= CD$.求证:$\angle B= \angle D$.
答案:证明:在△ABC和△ADC中,
{AB=AD,
BC=DC,
AC=AC,
∴△ABC≌△ADC(SSS),∴∠B=∠D.
3. (2024·江宁区模拟)如图是小明制作的风筝,他根据$DE= DF$,$EH= FH$,不用测量,就知道$\angle DEH= \angle DFH$.小明是通过全等三角形的知识得到的结论,请帮他说明理由.

答案:解:在△DHE和△DHF中,
{DH=DH,
DE=DF,
EH=FH,
∴△DHE≌△DHF(SSS),∴∠DEH=∠DFH.