1.
斜边
和一直角边
分别相等
的两个直角三角形全等(可以简写成
斜边、直角边
或
HL
).
答案:斜边 分别相等 斜边、直角边 HL
如图,在$Rt△ABC和Rt△DEF$中,
$\left\{\begin{array}{l} AB= \underline{
DE
}\\ \underline{
AC
}=DF,\end{array} \right.$
$\therefore Rt△ABC\cong Rt△DEF$(
HL
).
答案:DE AC HL
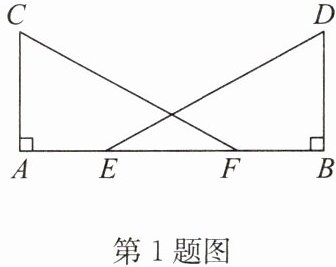
1. 如图,点A,E,F,B在同一条直线上,$CA⊥AB,DB⊥AB,AE= FB,CF= DE.$
求证:$∠AFC= ∠BED.$
答案:证明:∵AE=BF,
∴AE+EF=BF+EF,即AF=BE.
∵CF=DE,∠A=∠B=90°,
∴Rt△ACF≌Rt△BDE(HL).
∴∠AFC=∠BED.
2. (朝阳区期末)如图,$AB= CD,BE⊥AC$于点E,$DF⊥AC$于点F,$AF= CE.$
(1)求证:$△ABE\cong △CDF;$
(2)求证:$AB// CD.$

答案:(1)证明:∵BE⊥AC于点E,DF⊥AC于点F,
∴∠AEB=∠CFD=90°.
∵AF=CE,∴AF-EF=CE-EF,即AE=CF.
在Rt△ABE和Rt△CDF中,{AB=CD,
AE=CF,
∴Rt△ABE≌Rt△CDF(HL).
(2)∵△ABE≌△CDF,∴∠A=∠C,
∴AB//CD.
3. 如图,$AB⊥EF$于点B,$CD⊥EF$于点D,$BE= DF$. 若要用“HL”判定$Rt△ABF\cong Rt△CDE$,请写出需要添加的条件,并说明理由.

答案:解:添加的条件为AF=CE.理由如下:
∵BE=DF,∴BE+BD=DF+BD,即DE=BF.
∵AB⊥EF于点B,CD⊥EF于点D,
∴∠ABF=∠CDE=90°.
在Rt△ABF和Rt△CDE中,{AF=CE,
BF=DE,
∴Rt△ABF≌Rt△CDE(HL).