3. 如图①,$\triangle ABC与\triangle DEF$都是等腰直角三角形,$\angle ACB = \angle EDF = 90^{\circ}$,$AB$,$EF的中点均为点O$, 连接$CD$.
(1) 求证:$CD = BF$;
(2) 如图②, 在$\triangle DEF绕点O$顺时针旋转的过程中, 探究$BF与CD$之间的数量关系和位置关系, 并证明.
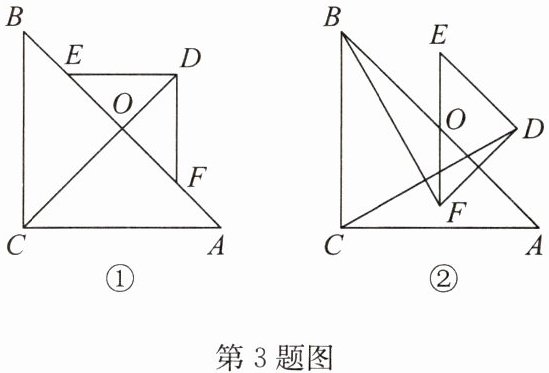
答案:(1) 证明:$\because \triangle ABC$ 与 $\triangle DEF$ 都是等腰直角三角形,$AB$,$EF$ 的中点均为 $O$,$\therefore CD$ 必过点 $O$,
$\therefore CO = BO$,$OD = OF$,
$\therefore CD = OC + OD = OB + OF = BF$。
(2) 解:$BF = CD$,$BF \perp CD$。
证明如下:
连接 $OC$,$OD$,$OC$ 交 $BF$ 于点 $G$,$BF$ 与 $CD$ 相交于点 $H$,如答图。
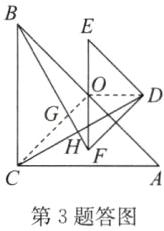
$\because \triangle ABC$ 与 $\triangle DEF$ 都是等腰直角三角形,$AB$,$EF$ 的中点均为 $O$,
$\therefore OC \perp AB$,$OD \perp EF$,
$\therefore \angle BOC = 90^{\circ}$,$\angle DOF = 90^{\circ}$,$\therefore \angle BOF = \angle DOC$。
在 $\triangle BOF$ 和 $\triangle COD$ 中,$\left\{\begin{array}{l} OB = OC, \\ \angle BOF = \angle COD, \\ OF = OD, \end{array}\right.$
$\therefore \triangle BOF \cong \triangle COD$,$\therefore BF = CD$,$\angle OBF = \angle OCD$。
又 $\angle CGH = \angle BGO$,
$\therefore \angle CHB = \angle COB = 90^{\circ}$,$\therefore BF \perp CD$。