1. 在$\triangle ABC$中,$\angle BAC= 40^{\circ }$,D 是边 AB 上的一点,将$\triangle BCD$沿直线 CD 翻折,使点 B 落在边 AC 上的点 E 处. 如果$\triangle ADE$是等腰三角形,那么$\angle ABC= $____$^{\circ }$.
答案:80或110 点拨:若△ADE是等腰三角形,则AE=DE 或AE=AD或AD=ED.
如答图①,当AE=DE时,∠BAC=∠ADE.
∵∠BAC=40°,∴∠ADE=40°.
∵∠CED是△AED的外角,
∴∠CED=∠BAC+∠ADE=40°+40°=80°.
由翻折的性质得∠ABC=∠CED=80°.
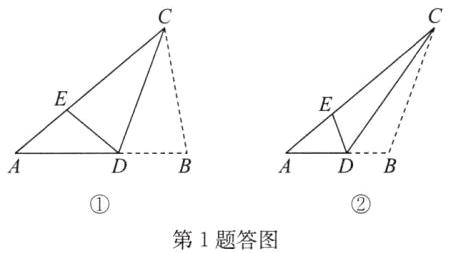
如答图②,当AE=AD时,∠AED=∠ADE.
∵∠BAC=40°,
∴∠AED=∠ADE=$\frac{180°−40°}{2}$=70°,
∴∠CED=180°−∠AED=180°−70°=110°.
由翻折的性质得∠ABC=∠CED=110°.
当AD=ED时,∠AED=∠BAC=40°,
∴∠CED=180°−∠AED=180°−40°=140°.
由翻折的性质得∠ABC=∠CED=140°.
此时∠BAC+∠ABC=180°,不符合题意,舍去.
综上,∠ABC的度数为80°或110°.
2. 在$\triangle ABC$中,$AB= AC$.
(1)如图①,若$\angle BAD= 40^{\circ },AD是\triangle ABC$的中线,$AD= AE$,求$\angle EDC$的度数;
(2)如图②,若$\angle BAD= 70^{\circ },AD是\triangle ABC$的中线,$AD= AE$,则$\angle EDC= $____$^{\circ }$;
(3)思考,通过以上两题,你发现$\angle BAD与\angle EDC$之间有什么数量关系? 用式子表示为____;
(4)如图③,如果 AD 不是$\triangle ABC$的中线,$AD= AE$,是否仍有上述关系? 请说明理由.
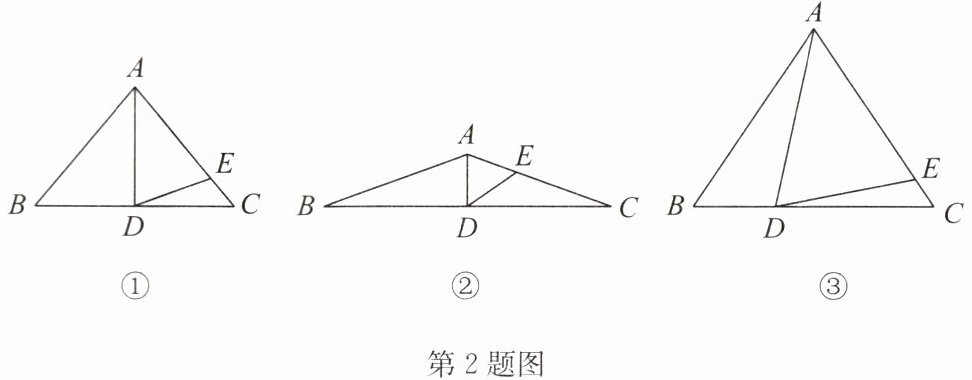
答案:(1)解:∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,∠CAD=∠BAD=40°,∴∠ADC=90°.
∵AD=AE,
∴∠ADE=$\frac{1}{2}$(180°−∠CAD)=$\frac{1}{2}$×(180°−40°)=70°,∴∠EDC=∠ADC−∠ADE=90°−70°=20°.
(2) 35
(3)∠BAD=2∠EDC
(4)解:有.理由如下:
如答图,∵AB=AC,AD=AE,
∴∠B=∠C,∠1=∠2.
∵∠1+∠3=∠4+∠B,∠2=∠3+∠C,
∴∠4=2∠3,即∠BAD=2∠EDC.

3. 如图,O 是等边$\triangle ABC$内一点,$\angle AOB= 110^{\circ },\angle BOC= \alpha$,将$\triangle BOC$绕点 C 沿顺时针方向旋转$60^{\circ }$,得到$\triangle ADC$,连接 OD.
(1)求证:$\triangle COD$是等边三角形;
(2)当$\alpha =150^{\circ }$时,试判断$\triangle AOD$的形状,并说明理由;
(3)探索:当α为多少度时,$\triangle AOD$是等腰三角形.

答案:(1)证明:由旋转的性质得CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)解:当α=150°,即∠BOC=150°时,△AOD是直角三角形.理由如下:
由旋转的性质得△BOC≌△ADC,
∴∠ADC=∠BOC=150°.
又∵△COD是等边三角形,
∴∠ODC=60°,∴∠ADO=90°,
即△AOD是直角三角形.
(3)解:分三种情况:
①当AO=AD时,∠AOD=∠ADO.
∵∠AOD=360°−∠AOB−∠COD−α=360°−110°−60°−α=190°−α,∠ADO=α−60°,
∴190°−α=α−60°,∴α=125°.
②当OA=OD时,∠OAD=∠ADO.
∵∠AOD=190°−α,∠ADO=α−60°,
∴∠OAD=180°−(∠AOD+∠ADO)=50°,
∴α−60°=50°,∴α=110°.
③当OD=AD时,∠OAD=∠AOD.
∵190°−α=50°,∴α=140°.
综上所述,当α为125°或110°或140°时,△AOD是等腰三角形.