2025年启东中学作业本八年级数学上册人教版第16页解析答案

1. 如图,已知 $ Rt\triangle OAB $,$ \angle OAB = 60^{\circ} $,$ \angle AOB = 90^{\circ} $,$ O $ 点与平面直角坐标系的原点重合,若点 $ P $ 在 $ x $ 轴上,且 $ \triangle APB $ 是等腰三角形,则满足条件的点 $ P $ 的个数是 (

)

A.1
B.2
C.3
D.4

答案：D

解析：

解：设 $ OA = 1 $。
在 $ Rt\triangle OAB $ 中，$\angle OAB = 60^\circ$，$\angle AOB = 90^\circ$，则$\angle ABO = 30^\circ$，$ AB = 2OA = 2 $，$ OB = OA \tan 60^\circ = \sqrt{3} $。
$\therefore A(0,1)$，$ B(-\sqrt{3},0) $。
设 $ P(x,0) $。
情况1：$ AP = BP $
$ \sqrt{x^2 + 1^2} = |x + \sqrt{3}| $
解得 $ x = \frac{\sqrt{3}}{3} $，$ P\left( \frac{\sqrt{3}}{3}, 0 \right) $。
情况2：$ AP = AB = 2 $
$ \sqrt{x^2 + 1^2} = 2 $
解得 $ x = \sqrt{3} $ 或 $ x = -\sqrt{3} $（$ x = -\sqrt{3} $ 与 $ B $ 重合，舍去），$ P(\sqrt{3}, 0) $。
情况3：$ BP = AB = 2 $
$ |x + \sqrt{3}| = 2 $
解得 $ x = 2 - \sqrt{3} $ 或 $ x = -2 - \sqrt{3} $，$ P(2 - \sqrt{3}, 0) $，$ P(-2 - \sqrt{3}, 0) $。
综上，满足条件的点 $ P $ 共4个。
答案：D

2. (2024 春·酒泉期末)如图,在由边长为 1 的小正方形组成的 $ 5 × 5 $ 的网格中,点 $ A $,$ B $ 在小方格的顶点上,要在小方格的顶点处确定一点 $ C $,连接 $ AC $ 和 $ BC $,使 $ \triangle ABC $ 是等腰三角形,则方格图中满足条件的点 $ C $ 有

个.

答案：6

解析：

解：以A为顶点，AB为腰：在网格中找到与B关于AB中垂线对称或到A距离等于AB的点，有2个；
以B为顶点，AB为腰：同理找到到B距离等于AB的点，有2个；
以AB为底边：作AB的垂直平分线，与网格顶点交点有2个；
共2+2+2=6个。
答案：6

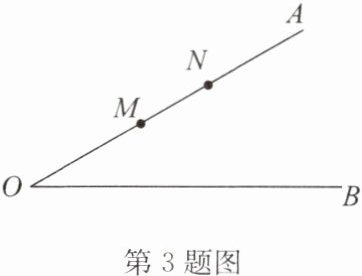
3. 如图,$ M $,$ N $ 是 $ \angle AOB $ 的边 $ OA $ 上的两个点 $ (OM \lt ON) $,$ \angle AOB = 30^{\circ} $,$ OM = a $,$ MN = 4 $. 若边 $ OB $ 上有且只有 1 个点 $ P $,满足 $ \triangle PMN $ 是等腰三角形,求 $ a $ 的取值范围.

答案：
解:①作线段MN的垂直平分线交OB于点P，连接PM,PN,如答图.
　　　　　　

此时 $ PM = PN $，$ \triangle PMN $ 是等腰三角形。
过点 M 作 $ MH \perp OB $ 于点 H，如答图。
当 $ MH ＞ MN $ 时，满足条件的点 P 恰好只有一个。
$ \because MN = 4 $，$ \angle AOB = 30^{\circ} $，
又当 $ MH = 4 $ 时，$ OM = 2MH = 8 $，
$ \therefore $ 当 $ a ＞ 8 $ 时，满足条件的点 P 恰好只有一个。
②当 $ \triangle PMN $ 是等边三角形时，满足条件的点 P 恰好只有一个，
此时 $ MN = MP $，$ \angle NMP = 60^{\circ} $。
$ \because \angle AOB = 30^{\circ} $，$ \therefore \angle MPO = 30^{\circ} $，
$ \therefore OM = MP = MN = 4 $，$ \therefore a = 4 $。
综上，满足条件的 a 的取值范围为 $ a = 4 $ 或 $ a ＞ 8 $。