2025年启东中学作业本八年级数学上册人教版第15页解析答案

1. 如图,已知在四边形 $ABCD$ 内,$DB = DC$,$\angle DCA = 60^{\circ}$,$\angle DAC = 78^{\circ}$,$\angle CAB = 24^{\circ}$,则 $\angle ACB$ 的度数为______。

答案：
$18^{\circ}$ 点拨: 如图, 延长 $CA$ 到点 $E$ 使 $AE = AB$, 连接 $DE$.
$\because \angle DAC = 78^{\circ}$, $\therefore \angle DAE = 102^{\circ}$,
$\because \angle DAB = \angle DAC + \angle CAB = 78^{\circ} + 24^{\circ} = 102^{\circ}$,
$\therefore \angle DAE = \angle DAB$,
$\because DA = DA$, $\therefore \triangle DAB \cong \triangle DAE(SAS)$,
$\therefore DE = DB = DC$,
$\because \angle DCA = 60^{\circ}$, $\therefore \triangle DEC$ 是等边三角形,
$\therefore \angle EDC = 60^{\circ}$,
$\because \angle ADC = 180^{\circ} - 78^{\circ} - 60^{\circ} = 42^{\circ}$,
$\therefore \angle EDA = 60^{\circ} - 42^{\circ} = 18^{\circ}$,
$\therefore \angle ADB = \angle EDA = 18^{\circ}$,
$\therefore \angle BDC = 60^{\circ} - 2 × 18^{\circ} = 24^{\circ}$,
$\therefore \angle DBC = \angle DCB = \frac{1}{2} × (180^{\circ} - 24^{\circ}) = 78^{\circ}$,
$\therefore \angle ACB = 78^{\circ} - 60^{\circ} = 18^{\circ}$.

2. 如图,在 $\triangle ABC$ 中,$AB = AC$,点 $D$,$E$ 分别在 $BC$,$AC$ 的延长线上,$AD = AE$,$\angle CDE = 30^{\circ}$。
(1) 如果设 $\angle B = x^{\circ}$,用含 $x$ 的代数式表示 $\angle E$,并说明理由；
(2) 求 $\angle BAD$ 的度数。

答案：解: (1) $\angle E = 150^{\circ} - x^{\circ}$. 理由:
$\because AB = AC$, $\therefore \angle B = \angle ACB = x^{\circ}$.
$\because$ 点 $D$, $E$ 分别在 $BC$, $AC$ 的延长线上,
$\therefore \angle ACB = \angle DCE = x^{\circ}$,
$\therefore \angle E = 180^{\circ} - x^{\circ} - 30^{\circ} = 150^{\circ} - x^{\circ}$.
(2) $\because AD = AE$, $\therefore \angle ADE = \angle E = 150^{\circ} - x^{\circ}$,
$\therefore \angle EAD = 180^{\circ} - 2(150^{\circ} - x^{\circ})$.
$\because AB = AC$, $\therefore \angle BAC = 180^{\circ} - 2x^{\circ}$,
$\therefore \angle BAD = \angle BAC + \angle EAD = 180^{\circ} - 2x^{\circ} + 180^{\circ} - 300^{\circ} + 2x^{\circ} = 60^{\circ}$.

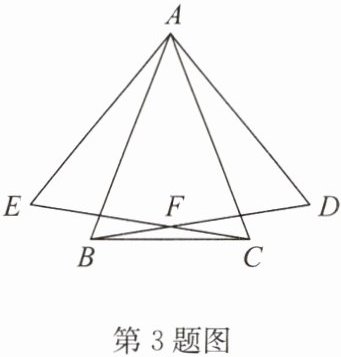
3. 如图,$\triangle ABC$ 是等腰三角形,$AB = AC$,$0^{\circ} ＜ \angle BAC ＜ 60^{\circ}$,分别在 $AB$ 的右侧,$AC$ 的左侧作等边三角形 $ABD$ 和等边三角形 $ACE$,$BD$ 与 $CE$ 相交于点 $F$。
(1) 求证：$BF = CF$。
(2) 作射线 $AF$ 交 $BC$ 于点 $G$,交射线 $DC$ 于点 $H$。
① 补全图形,当 $\angle BAC = 40^{\circ}$ 时,求 $\angle AHD$ 的度数。
② 当 $\angle BAC$ 的度数在给定范围内发生变化时,$\angle AHD$ 的度数是否也发生变化？若不变,请直接写出 $\angle AHD$ 的度数；若变化,请给出 $\angle AHD$ 的度数的变化范围。

答案：
(1) 证明: $\because AB = AC$, $\therefore \angle ACB = \angle ABC$.
$\because$ 三角形 $ABD$ 和三角形 $ACE$ 都是等边三角形,
$\therefore \angle ACE = \angle ABD = 60^{\circ}$.
$\because 0^{\circ} ＜ \angle BAC ＜ 60^{\circ}$,
$\therefore \angle ACB - \angle ACE = \angle ABC - \angle ABD$, 即 $\angle FBC = \angle FCB$,
$\therefore BF = CF$.
(2) 解: ① 补全图形如答图所示.
由 (1) 可得 $FB = FC$,
$\because AB = AC$, $\therefore AH$ 垂直平分 $BC$.
$\because \angle BAC = 40^{\circ}$, $\therefore \angle HAC = \frac{1}{2} \angle BAC = 20^{\circ}$.
$\because \angle BAC = 40^{\circ}$, $\angle BAD = 60^{\circ}$,
$\therefore \angle CAD = \angle BAD - \angle BAC = 60^{\circ} - 40^{\circ} = 20^{\circ}$,
$\therefore \angle HAD = \angle HAC + \angle CAD = 20^{\circ} + 20^{\circ} = 40^{\circ}$.
$\because AD = AB$, $AB = AC$, $\therefore AC = AD$,
$\therefore \angle ADC = \angle ACD = \frac{1}{2}(180^{\circ} - \angle CAD) = \frac{1}{2} × (180^{\circ} - 20^{\circ}) = 80^{\circ}$,
在 $\triangle AHD$ 中, $\angle AHD = 180^{\circ} - \angle HAD - \angle ADH = 180^{\circ} - 40^{\circ} - 80^{\circ} = 60^{\circ}$.

② 不变, $\angle AHD = 60^{\circ}$.