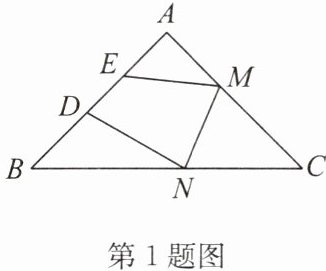
1. (2024春·罗湖区期末)如图,在△ABC中,AB= AC,∠A= 90°,点D,E是边AB上的两个定点,点M,N分别是边AC,BC上的两个动点. 当四边形DEMN的周长最小时,∠DNM+∠EMN的大小是 (
B
)
A.45°
B.90°
C.75°
D.135°
答案:B
解析:
解:作点D关于BC的对称点D',点E关于AC的对称点E',连接D'E',分别交AC、BC于点M、N。此时四边形DEMN周长最小。
由对称性质得:∠DNB=∠D'NB,∠EMC=∠E'MC。
∵AB=AC,∠A=90°,∴∠B=∠C=45°。
∵D'是D关于BC的对称点,∴∠D'BC=∠B=45°,∴∠D'BA=90°。
同理,∠E'CA=∠C=45°,∠E'AC=90°,∴E'在BA延长线上,D'E'//AC。
∴∠DNM=∠D',∠EMN=∠E'。
∵∠D' + ∠E' = 90°(D'E'//AC,∠A=90°),∴∠DNM + ∠EMN=90°。
答案:B
2. 如图,点P在∠AOB的内部,点C和点P关于OA对称,点P和点D关于OB对称,连接CD交OA于点M,交OB于点N,连接OP,PM,PN.
(1)①若∠AOB= 60°,求∠COD的度数;
②若∠AOB= n°,则∠COD=
2n
°. (用含n的代数式表示)
(2)若CD= 4,则△PMN的周长为
4
.

答案:(1)①解:∵点C和点P关于OA对称,
∴∠AOC=∠AOP.
∵点P和点D关于OB对称,
∴∠BOD=∠BOP.
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°.
②2n
(2)4 点拨:∵点C和点P关于OA对称,∴CM=PM.∵点P和点D关于OB对称,∴DN=PN.
∵CD=4,∴CM+MN+DN=4.
∴PM+MN+PN=4,
即△PMN的周长为4.
3. 如图,在△ABC中,∠ABC= 45°,点A关于直线BC的对称点为点P,连接PB并延长,过点C作CD⊥AC,交射线PB于点D.
(1)如图①,当∠ACB为钝角时,补全图形,判断AC与CD的数量关系为______;
(2)如图②,当∠ACB为锐角时,(1)中的结论是否仍成立? 请说明理由.

答案:解:(1)补全图形如答图①. AC=CD
点拨:如答图①,连接CP,设AB交CD于点O.
∵点A,P关于直线BC对称,
∴CA=CP,∠A=∠P,∠ABC=∠CBP=45°,
∴∠ABP=∠ABD=90°.
∵AC⊥CD,∴∠ACO=∠DBO=90°.
∵∠AOC=∠DOB,∴∠D=∠A,∴∠D=∠P,
∴CD=CP,∴AC=CD.

(2)(1)中结论仍成立.
理由:如答图②,连接CP.
∵点A,P关于直线BC对称,
∴CA=CP,∠A=∠P,∠ABC=∠CBP=45°,
∴∠ABP=90°.
∵AC⊥CD,∴∠ACD=90°,
∴∠ABD+∠ACD=180°,
∴∠A+∠BDC=180°.
∵∠CDP+∠BDC=180°,
∴∠A=∠CDP,∴∠CDP=∠P,
∴CD=CP,∴AC=CD.