2025年启东中学作业本八年级数学上册人教版第13页解析答案

1. 如图,已知$\triangle ABC的面积为8cm^{2}$,$BP为\angle ABC$的平分线,$AP垂直BP于点P$,则$\triangle BCP$的面积为(

)
A.$3.5cm^{2}$
B.$3.9cm^{2}$
C.$4cm^{2}$
D.$4.2cm^{2}$

答案：C

2. (2024 春·高州市月考)如图,$\triangle ABC$中,$\angle C = 90^{\circ}$,$AD是\triangle ABC$的角平分线,$DE\perp AB于点E$,$AD = BD$。
(1)求证：$AC = BE$；(2)求$\angle B$的度数。

答案：【解析】：本题可根据角平分线的性质、全等三角形的判定与性质以及等腰三角形的性质来求解。
（1）求证$AC = BE$：
因为$AD$是$\triangle ABC$的角平分线，$\angle C = 90^{\circ}$（即$DC\perp AC$），$DE\perp AB$，根据角平分线的性质：角平分线上的点到角两边的距离相等，可得$DC = DE$。
在$Rt\triangle ACD$和$Rt\triangle AED$中，$\begin{cases}AD = AD\\DC = DE\end{cases}$，根据“$HL$”（斜边和一条直角边对应相等的两个直角三角形全等）可判定$Rt\triangle ACD\cong Rt\triangle AED$，再根据全等三角形的性质：全等三角形的对应边相等，所以$AC = AE$。
又因为$AD = BD$，$DE\perp AB$，根据等腰三角形“三线合一”的性质（等腰三角形底边上的高、底边上的中线、顶角平分线相互重合），可知$BE = AE$。
由于$AC = AE$，$BE = AE$，所以$AC = BE$。
（2）求$\angle B$的度数：
由$AD = BD$，根据等腰三角形的性质：等腰三角形的两个底角相等，可得$\angle B = \angle BAD$。
因为$AD$是$\angle BAC$的角平分线，所以$\angle CAD = \angle BAD$。
那么$\angle B = \angle BAD = \angle CAD$。
在$\triangle ABC$中，$\angle C = 90^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle B + \angle BAC = 180^{\circ} - \angle C = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
又因为$\angle BAC = \angle BAD + \angle CAD = 2\angle B$，所以$\angle B + 2\angle B = 90^{\circ}$，即$3\angle B = 90^{\circ}$，解得$\angle B = 30^{\circ}$。
【答案】：(1) 证明：
∵$AD$是$\triangle ABC$的角平分线，$\angle C = 90^{\circ}$，$DE\perp AB$，
∴$DC = DE$。
在$Rt\triangle ACD$和$Rt\triangle AED$中，$\begin{cases}AD = AD\\DC = DE\end{cases}$，
∴$Rt\triangle ACD\cong Rt\triangle AED(HL)$，
∴$AC = AE$。
∵$AD = BD$，$DE\perp AB$，
∴$BE = AE$，
∴$AC = BE$。
(2)
∵$AD = BD$，
∴$\angle B = \angle BAD$。
∵$AD$是$\angle BAC$的角平分线，
∴$\angle CAD = \angle BAD$。
∴$\angle B = \angle BAD = \angle CAD$。
∵$\angle C = 90^{\circ}$，
∴$\angle B + \angle BAC = 180^{\circ} - \angle C = 90^{\circ}$，
又∵$\angle BAC = \angle BAD + \angle CAD = 2\angle B$，
∴$\angle B + 2\angle B = 90^{\circ}$，
即$3\angle B = 90^{\circ}$，
解得$\angle B = 30^{\circ}$。

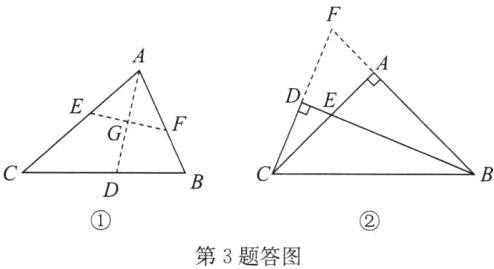
3. (1)观察与发现：小明将三角形纸片$ABC(AC＞AB)沿过点A$的直线折叠,使得$AB落在AC$边上,折痕为$AD$,展平纸片(如图①)；在第一次折叠的基础上,第二次折叠该三角形纸片,使点$A和点D$重合,折痕为$EF$,展平纸片后得到$\triangle AEF$(如图②)。小明认为$\triangle AEF$是等腰三角形,你同意他的结论吗？请说明理由。
(2)模型与运用：如图③,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$,$BE平分\angle ABC交AC于点E$,过点$C作CD\perp BE$,交$BE的延长线于点D$。若$CD = 4$,求$\triangle BCE$的面积。

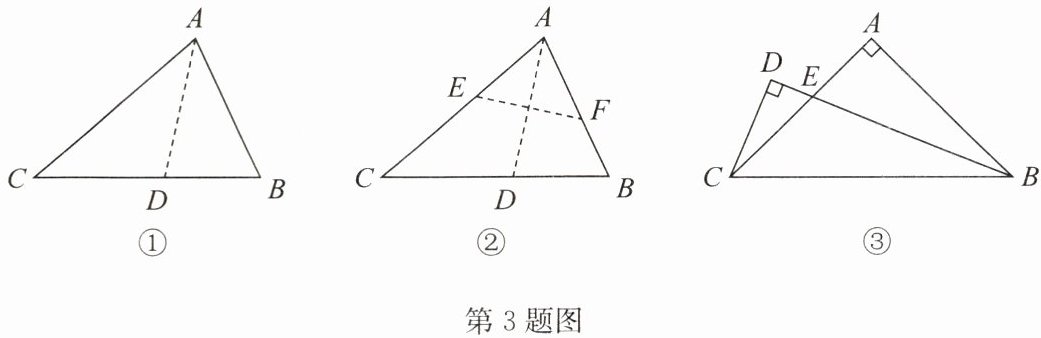
答案：
3. 解:(1)同意.理由如下:
如答图①,设AD与EF交于点G.
由折叠知,AD平分∠BAC,∴∠BAD=∠CAD.
由折叠知,∠AGE=∠DGE,∴∠AGE=∠AGF=90°,
∴∠AEF=∠AFE,∴AE=AF,
即△AEF为等腰三角形.
(2)如答图②,延长CD与BA,交于点F.
∵BE平分∠ABC,CD⊥BE,
∴∠ABD=∠CBD,∠BDF=∠BDC=90°,
又∵BD=BD,∴△BDF≌△BDC(ASA),
∴FD=CD=4,CF=2CD=8.
∵∠BAC=90°,∴∠ABD+∠AEB=90°.
∵CD⊥BD,∴∠EDC=90°,∴∠ACD+∠CED=90°.
∵∠AEB=∠CED,∴∠ACD=∠ABD.
∵AC=AB,∴△CAF≌△BAE(ASA),∴BE=CF=8,
∴$S _ { △ B C E } = \frac { 1 } { 2 } B E \cdot C D = \frac { 1 } { 2 } × 8 × 4 = 16.$