答案：
1. A 点拨:在BA的延长线上取点E,使AE = AC，连接EP,如答图。

∵AD是△BAC的外角平分线，∴∠CAD = ∠EAD。
在△ACP和△AEP中，$\left\{ \begin{array} { l } { AC = AE, } \\ { \angle CAP = \angle EAP, } \\ { AP = AP, } \end{array} \right.$
∴△ACP≌△AEP(SAS)，∴PE = PC。
在△PBE中，PB + PE＞AB + AE。
∵PB = m，PC = n，AB = c，AC = b，∴m + n＞b + c。

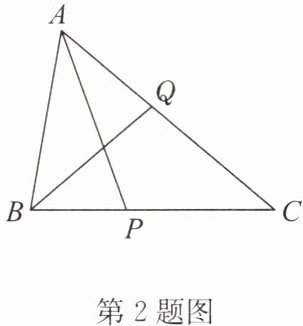
答案：
2. 证明:方法一:延长AB到点D，使BD = BP，连接PD，如答图①，则∠D = ∠5。
∵AP、BQ分别是∠BAC、∠ABC的平分线，∠BAC = 60°，∠C = 40°，
∴∠1 = ∠2 = 30°，∠ABC = 180° - 60° - 40° = 80°，∠3 = ∠4 = 40° = ∠C，∴QB = QC。
又∠D + ∠5 = ∠3 + ∠4 = 80°，∴∠D = 40°。
在△APD与△APC中，
$\left\{ \begin{array} { l } { \angle D = \angle C, } \\ { \angle 2 = \angle 1, } \\ { AP = AP, } \end{array} \right.$
∴△APD≌△APC(AAS)，∴AD = AC，
即AB + BD = AQ + QC，∴AB + BP = BQ + AQ。

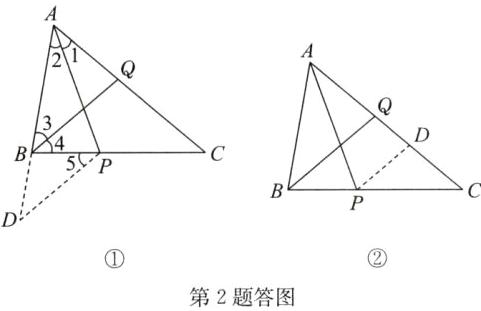
方法二:易得∠CBQ = $\frac{1}{2}$∠ABC = $\frac{1}{2}$×(180° - 60° - 40°) = 40°，
∴∠CBQ = ∠C，∴BQ = CQ，
∴BQ + AQ = CQ + AQ = AC①。
过点P作PD//BQ交CQ于点D，如答图②，
则∠CPD = ∠CBQ = 40°，∴∠CPD = ∠C = 40°，
∴PD = CD，∠ADP = ∠CPD + ∠C = 40° + 40° = 80°。
∵∠ABC = 80°，∴∠ABC = ∠ADP。
∵AP平分∠BAC，∴∠BAP = ∠CAP。
在△ABP与△ADP中，
$\left\{ \begin{array} { l } { \angle ABP = \angle ADP, } \\ { \angle BAP = \angle DAP, } \\ { AP = AP, } \end{array} \right.$
∴△ABP≌△ADP(AAS)，
∴AB = AD，BP = PD，
∴AB + BP = AD + PD = AD + CD = AC②。
由①②可得，AB + BP = BQ + AQ。

答案：
3. (1) 证明:如答图①，在BC上截取BD = BA。

∵BE平分∠ABC，∴∠EBA = ∠EBD。
∵BA = BD，BE = BE，
∴△BEA≌△BED(SAS)，∴∠A = ∠BDE = 108°。
∵AB = AC，∴∠C = ∠ABC = 36°，∠EDC = 72°，
∴∠CED = 72°，∴CE = CD，
∴BC = BD + CD = AB + CE。
(2) 解:不成立。结论:BC = BE + AE。
证明:如答图②，在射线BC、BA上分别截取BF = BE，BH = BE，可证△EBH≌△EBF，∴EF = EH。
∵∠BAC = 100°，AB = AC，∴∠ABC = ∠C = 40°，
∴∠EBA = ∠EBC = 20°，
∴∠BFE = ∠H = ∠EAH = 80°，∴AE = EH。
∵∠BFE = ∠C + ∠FEC，
∴∠CEF = ∠C = 40°，∴EF = CF，∴CF = AE，
∴BC = BF + CF = BE + AE。