2. (2024 春·佛山月考) 如图,在四边形 $ABCD$ 中,$AB = AD$,$CA$ 平分 $\angle BCD$,$AE\perp BC$ 于点 $E$。求证:$BE + CD = CE$。
答案:证明:方法一:如答图①,在CE上截取CF=CD,连接AF;
∵CA平分∠BCD,∴∠ACD = ∠ACF,
∵CF = CD,AC = AC,∴△CAD ≌ △CAF(SAS),
∴AD = AF = AB.
∵AE⊥BC,∴∠AEB = ∠AEF = 90°,
∵AB = AF,AE = AE,∴Rt△ABE ≌ Rt△AFE(HL),
∴BE = EF,∴BE + CD = EF + CF = CE;
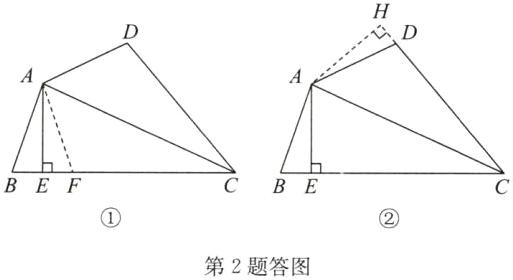
方法二:如答图②,过点A作AH⊥CD,交CD的延长线于点H,
∵CA平分∠BCD,AE⊥BC,∴AE = AH,
易证Rt△ABE ≌ Rt△ADH(HL),
Rt△ACE ≌ Rt△ACH(HL),
∴BE = DH,CE = CH,
∴BE + CD = DH + CD = CH = CE.