2025年启东中学作业本八年级数学上册人教版第10页解析答案

1. 已知,如图,$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,$D为BC$上一点,$CE\perp AD于点E$,连接$BE$,若$CE = 2$,则$S_{\triangle BEC}= $

答案：2　点拨:过点B作$BH⊥CE$交CE的延长线于点H.
$\because ∠ACB=90^{\circ },\therefore ∠ACE+∠BCH=90^{\circ }.$
$\because BH⊥CE,\therefore ∠BHC=90^{\circ },$
$\therefore ∠HBC+∠BCH=90^{\circ },\therefore ∠HBC=∠ACE.$
在$△BHC$与$△CEA$中,
$\left\{\begin{array}{l} ∠BHC=∠CEA=90^{\circ },\\ ∠HBC=∠ECA,\\ BC=CA,\end{array}\right.$
$\therefore △BHC\cong △CEA(AAS),$
$\therefore BH=CE=2,$
$\therefore S_{△BEC}=\frac {CE\cdot BH}{2}=\frac {2×2}{2}=2.$

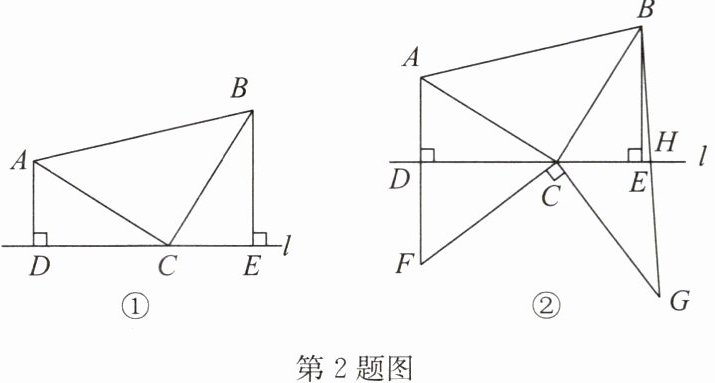
2. 如图①,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,直线$l经过点C$,过点$A作AD\perp l$,垂足为$D$,过点$B作BE\perp l$,垂足为$E$.
(1)求证:$\triangle ADC\cong\triangle CEB$;
(2)若$AD = 5$,$DE = 13$,求$BE$的长;
(3)如图②,延长$AD至点F$,连接$CF$,过点$C作CG\perp CF$,且$CG = CF$,连接$BG交直线l于点H$,若$S_{\triangle CGH}= 30$,$CD = 10$,则$AF= $____.

答案：
(1)证明:$\because AD⊥DE,BE⊥DE,$
$\therefore ∠ADC=∠CEB=∠ACB=90^{\circ }.$
$\therefore ∠DAC+∠DCA=∠ECB+∠DCA=90^{\circ },$
$\therefore ∠DAC=∠ECB.$
在$△ADC$和$△CEB$中,
$\left\{\begin{array}{l} ∠ADC=∠CEB,\\ ∠DAC=∠ECB,\\ AC=CB,\end{array}\right.$
$\therefore △ADC\cong △CEB(AAS).$
(2)解:$\because △ADC\cong △CEB,AD=5,$
$\therefore AD=CE=5,$$CD=BE.$
$\because DE=13,\therefore BE=CD=13 - 5=8.$
(3)12　点拨:过点G作$GM⊥l$于点M,如答图.

$\because CG⊥CF,$
$\therefore ∠CFD+∠DCF=∠DCF+∠MCG=90^{\circ },$
$\therefore ∠CFD=∠MCG.$
$\because ∠CDF=∠CMG=90^{\circ },CF=CG,$
$\therefore △CDF\cong △GMC(AAS),$
$\therefore CD=GM=10,DF=MC.$
$\because S_{△CGH}=30,$
$\therefore \frac {1}{2}CH\cdot GM=30,\therefore CH=\frac {2×30}{GM}=\frac {60}{10}=6.$
$\because △ACD\cong △CBE,\therefore CD=BE=10,AD=CE,$
$\therefore BE=GM.$
$\because ∠BEH=∠GMH=90^{\circ },∠BHE=∠GHM,$
$\therefore △BEH\cong △GMH(AAS),\therefore EH=MH,$
$\therefore AF=AD+DF=CE+CM=CH - EH+CH+EH=2CH=2×6=12.$