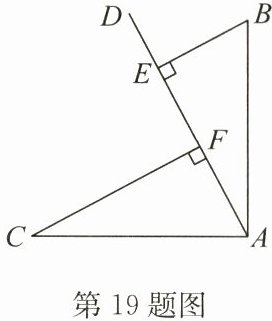
19. (6分)如图,已知$∠BAC= 90^{\circ }$,AD是$∠BAC$内部的一条射线,$AB= AC,BE⊥AD$于点E,$CF⊥AD$于点F,求证:$AF= BE$.
答案:解:因为$BE\perp AD$,$CF\perp AD$,所以$\angle AEB = \angle CFA = 90^{\circ}$。
又因为$\angle BAC = 90^{\circ}$,所以$\angle BAE+\angle CAF = 90^{\circ}$。
在$\triangle ABE$中,$\angle BAE+\angle ABE = 90^{\circ}$,所以$\angle ABE=\angle CAF$。
在$\triangle ABE$和$\triangle CAF$中,$\begin{cases}\angle AEB=\angle CFA\\\angle ABE = \angle CAF\\AB = AC\end{cases}$。
根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle ABE\cong\triangle CAF$。
因为全等三角形的对应边相等,所以$AF = BE$。
20. (6分)如图,BE是$△ABC$的角平分线,在AB上取点D,使$DB= DE$.若$∠A= 65^{\circ },∠AED= 45^{\circ }$,求$∠EBC$的度数.

答案:解:
1. 因为$DB = DE$,根据等腰三角形的性质:$\angle DBE=\angle DEB$。
又因为$BE$是$\triangle ABC$的角平分线,所以$\angle DBE=\angle EBC$,则$\angle DBE=\angle DEB = \angle EBC$。
2. 由三角形外角性质:$\angle ADE=\angle DBE+\angle DEB = 2\angle EBC$(三角形的一个外角等于与它不相邻的两个内角之和)。
已知$\angle A = 65^{\circ}$,$\angle AED = 45^{\circ}$。
在$\triangle ADE$中,根据三角形内角和定理$\angle A+\angle AED+\angle ADE = 180^{\circ}$(\三角形内角和为$180^{\circ}$)。
把$\angle A = 65^{\circ}$,$\angle AED = 45^{\circ}$代入可得:$\angle ADE=180^{\circ}-\angle A - \angle AED$。
即$\angle ADE=180^{\circ}-65^{\circ}-45^{\circ}=70^{\circ}$。
3. 因为$\angle ADE = 2\angle EBC$。
所以$\angle EBC=\frac{1}{2}\angle ADE$。
把$\angle ADE = 70^{\circ}$代入得$\angle EBC = 35^{\circ}$。
综上,$\angle EBC$的度数为$35^{\circ}$。
21. (8分)(1)已知$5x^{2}-x-1= 0$,求代数式$(3x+2)(3x-2)+x(x-2)$的值;
(2)先化简,再求值:$(x-1-\frac {x^{2}}{x+1})÷\frac {x}{x^{2}+2x+1}$,其中$x= 3$.
答案:$(1)$
解:
- **步骤一:化简代数式$(3x + 2)(3x - 2)+x(x - 2)$
根据平方差公式$(a+b)(a-b)=a^2-b^2$,对$(3x + 2)(3x - 2)$化简可得:
$(3x + 2)(3x - 2)=(3x)^2-2^2 = 9x^2-4$
再根据单项式乘多项式法则$a(b+c)=ab+ac$,对$x(x - 2)$化简可得:$x(x - 2)=x^2-2x$
所以$(3x + 2)(3x - 2)+x(x - 2)=9x^2-4+x^2-2x=10x^2-2x - 4$。
- **步骤二:由已知条件$5x^{2}-x - 1 = 0$得到$5x^{2}-x=1$,并对$10x^2-2x - 4$变形求值
对$10x^2-2x - 4$提取公因式$2$可得:$10x^2-2x - 4=2(5x^2-x)-4$
把$5x^{2}-x = 1$代入$2(5x^2-x)-4$得:$2×1 - 4=-2$。
$(2)$
解:
- **步骤一:化简$(x - 1-\frac{x^{2}}{x + 1})÷\frac{x}{x^{2}+2x + 1}$
先对括号内通分:
$x - 1-\frac{x^{2}}{x + 1}=\frac{(x - 1)(x + 1)-x^{2}}{x + 1}=\frac{x^{2}-1-x^{2}}{x + 1}=-\frac{1}{x + 1}$
再根据完全平方公式$(a+b)^2=a^2+2ab+b^2$,$x^{2}+2x + 1=(x + 1)^2$,则原式变为:
$(-\frac{1}{x + 1})÷\frac{x}{(x + 1)^2}=(-\frac{1}{x + 1})×\frac{(x + 1)^2}{x}=-\frac{x + 1}{x}$
- **步骤二:把$x = 3$代入化简后的式子求值
当$x = 3$时,$-\frac{x + 1}{x}=-\frac{3 + 1}{3}=-\frac{4}{3}$。
综上,$(1)$的值为$-2$;$(2)$化简后为$-\frac{x + 1}{x}$,值为$-\frac{4}{3}$。
解析:
(1) 解:$(3x + 2)(3x - 2) + x(x - 2)$
$=9x^2 - 4 + x^2 - 2x$
$=10x^2 - 2x - 4$
∵$5x^2 - x - 1 = 0$
∴$5x^2 - x = 1$
∴原式$=2(5x^2 - x) - 4 = 2×1 - 4 = -2$
(2) 解:$(x - 1 - \frac{x^2}{x + 1})÷\frac{x}{x^2 + 2x + 1}$
$=(\frac{(x - 1)(x + 1) - x^2}{x + 1})÷\frac{x}{(x + 1)^2}$
$=(\frac{x^2 - 1 - x^2}{x + 1})×\frac{(x + 1)^2}{x}$
$=\frac{-1}{x + 1}×\frac{(x + 1)^2}{x}$
$=-\frac{x + 1}{x}$
当$x = 3$时,原式$=-\frac{3 + 1}{3}=-\frac{4}{3}$
22. (6分)如图,B,C两点关于y轴对称,点A的坐标是$(0,b)$,点C的坐标为$(-a,-a-b)$.
(1)点B的坐标为______;
(2)用尺规作图,在x轴上作出点P,使得$AP+PB$的值最小;
(3)$∠OAP= $______$^{\circ }$.

答案:(1) (a, -a - b)(2) 解:如答图,点P即为所求.
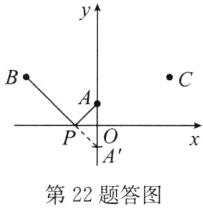
(3) 45
23. (6分)周六晚上小明打算和朋友乘出租车去某电影院看电影,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵;路线二的全程是30千米,平均速度比走路线一时的平均速度能提高80%,比走路线一少用10分钟到达.求小明走路线一时的平均速度.
答案:解:设小明走路线一时的平均速度是$x$千米/小时。
路线一的全程是$25$千米,根据时间$=$路程$÷$速度,则走路线一需要的时间为$\dfrac{25}{x}$小时。
路线二的平均速度比走路线一时的平均速度能提高$80\%$,那么路线二的速度是$(1 + 80\%)x=1.8x$千米/小时,路线二全程$30$千米,则走路线二需要的时间为$\dfrac{30}{1.8x}$小时。
已知路线二比路线一少用$10$分钟($10$分钟$=\dfrac{10}{60}=\dfrac{1}{6}$小时)到达,可列方程:
$\dfrac{25}{x}-\dfrac{30}{1.8x}=\dfrac{1}{6}$
方程两边同时乘以$1.8x$去分母得:
$25×1.8 - 30 = 1.8x×\dfrac{1}{6}$
$45 - 30 = 0.3x$
$15 = 0.3x$
解得$x = 50$。
检验:当$x = 50$时,$1.8x=1.8×50 = 90\neq0$,$x = 50$是原方程的解,且符合题意。
所以,小明走路线一时的平均速度是$50$千米/小时。