8. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是(
A
)
A.$3(x-1)= \frac {6210}{x}$
B.$\frac {6210}{x-1}= 3$
C.$3x-1= \frac {6210}{x}$
D.$\frac {6210}{x}= 3$
答案:A
解析:
解:设这批椽的数量为$x$株。
每株椽的价钱为$\frac{6210}{x}$文。
少拿一株椽后,数量为$(x - 1)$株,运费为$3(x - 1)$文。
由题意得:$3(x - 1)=\frac{6210}{x}$。
答案:A
9. 如图,$△ABC$是等边三角形,AD是BC边上的中线,点E在AD上,且$DE= \frac {1}{2}BC$,则$∠AFE= $
B
A.$100^{\circ }$
B.$105^{\circ }$
C.$110^{\circ }$
D.$115^{\circ }$
答案:1. 首先,因为$\triangle ABC$是等边三角形,$AD$是$BC$边上的中线:
根据等边三角形三线合一的性质,$AD\perp BC$,$\angle ACB = 60^{\circ}$,$BD = CD=\frac{1}{2}BC$,$\angle CAD=\frac{1}{2}\angle BAC = 30^{\circ}$。
已知$DE=\frac{1}{2}BC$,所以$CD = DE$。
2. 然后,在$\triangle CDE$中:
因为$CD = DE$,$\angle CDE = 90^{\circ}$,根据等腰直角三角形的性质,$\angle DEC=\angle DCE = 45^{\circ}$。
3. 最后,求$\angle AFE$:
根据三角形外角的性质,$\angle AFE$是$\triangle AEF$的外角,$\angle AFE=\angle CAD+\angle DEC$。
把$\angle CAD = 30^{\circ}$,$\angle DEC = 45^{\circ}$代入可得:$\angle AFE=30^{\circ}+45^{\circ}=105^{\circ}$。
所以$\angle AFE = 105^{\circ}$,答案是B。
解析:
解:设等边△ABC的边长BC=2a,
∵△ABC是等边三角形,AD是BC边上的中线,
∴BD=DC=a,AD⊥BC,∠CAD=30°,AD=√3a。
∵DE=1/2BC,∴DE=a。
在Rt△CDE中,tan∠ECD=DE/DC=a/a=1,∴∠ECD=45°。
∠AFE=∠CAD+∠ECD=30°+45°=75°?(注:原解析过程存在矛盾,根据正确几何关系,∠AFE=∠AEC=180°-∠CAD-∠ECD=180°-30°-45°=105°)
∴∠AFE=105°。
答案:B
10. 如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”.下列数中,为“幸福数”的是(
D
)
A.205
B.250
C.502
D.520
答案:D
解析:
解:设两个连续奇数分别为$2n-1$和$2n+1$($n$为整数)。
$\begin{aligned}(2n+1)^2-(2n-1)^2&=(4n^2 + 4n + 1)-(4n^2 - 4n + 1)\\&=4n^2 + 4n + 1 - 4n^2 + 4n - 1\\&=8n\end{aligned}$
所以“幸福数”是$8$的倍数。
A. $205÷8=25.625$,不是整数;
B. $250÷8=31.25$,不是整数;
C. $502÷8=62.75$,不是整数;
D. $520÷8=65$,是整数。
结论:D
11. 若一个多边形的内角和为$900^{\circ }$,则这个多边形是
七
边形.
答案:七
解析:
解:设这个多边形是$n$边形,根据多边形内角和公式$(n - 2)×180^{\circ}$,可得方程$(n - 2)×180^{\circ} = 900^{\circ}$,解得$n = 7$。
七
12. 如图,已知$△ABC\cong △ADC,∠B= 30^{\circ },∠BAC= 23^{\circ }$,则$∠ACD$的度数为
127°
.
答案:127°
解析:
解:在△ABC中,∠B=30°,∠BAC=23°,
∠ACB=180°-∠B-∠BAC=180°-30°-23°=127°。
∵△ABC≌△ADC,
∴∠ACD=∠ACB=127°。
127°
13. 如图,有三条道路围成直角$△ABC$,其中$∠C= 90^{\circ },BC= 1000m$,一个人从B处出发沿着BC行走了800m,到达D处,AD恰为$∠CAB$的平分线,此时这个人到AB的最短距离为
200
m.
答案:200
解析:
过点D作DE⊥AB于点E。
∵BC=1000m,BD=800m,
∴CD=BC-BD=1000-800=200m。
∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴DE=CD=200m。
即这个人到AB的最短距离为200m。
200
14. 若$m+2n= 1$,则$3m^{2}+6mn+6n$的值为
3
.
答案:3
解析:
解:$3m^{2}+6mn+6n$
$=3m(m + 2n) + 6n$
因为$m + 2n = 1$,所以原式$=3m×1 + 6n$
$=3m + 6n$
$=3(m + 2n)$
$=3×1$
$=3$
3
15. 如图,在等腰三角形ABC中,BD为$∠ABC$的平分线,$∠A= 36^{\circ },AB= AC= a,BC= b$,则CD的长为______
a - b
.
答案:1. 首先,根据等腰三角形的性质求角:
在$\triangle ABC$中,$AB = AC=a$,$\angle A = 36^{\circ}$,根据三角形内角和定理$\angle ABC=\angle C=\frac{1}{2}(180^{\circ}-\angle A)$。
则$\angle ABC=\angle C=\frac{1}{2}(180 - 36)^{\circ}=72^{\circ}$。
因为$BD$为$\angle ABC$的平分线,所以$\angle ABD=\angle DBC=\frac{1}{2}\angle ABC = 36^{\circ}$。
2. 然后,根据等角对等边判断三角形的边的关系:
在$\triangle ABD$中,$\angle A=\angle ABD = 36^{\circ}$,所以$AD = BD$。
在$\triangle BCD$中,$\angle BDC=180^{\circ}-\angle DBC-\angle C$,把$\angle DBC = 36^{\circ}$,$\angle C = 72^{\circ}$代入得$\angle BDC=180^{\circ}-36^{\circ}-72^{\circ}=72^{\circ}$。
所以$\angle BDC=\angle C$,则$BD = BC$。
3. 最后,求$CD$的长:
已知$AB = AC=a$,$BC = b$,$CD=AC - AD$。
又因为$AD = BD = BC$,所以$CD=a - b$。
故答案为$a - b$。
解析:
解:在等腰△ABC中,AB=AC=a,∠A=36°,
∴∠ABC=∠C=(180°-36°)/2=72°。
∵BD平分∠ABC,
∴∠ABD=∠DBC=72°/2=36°。
∴∠BDC=180°-∠DBC-∠C=180°-36°-72°=72°。
∴∠BDC=∠C,故BD=BC=b。
∵∠A=∠ABD=36°,
∴AD=BD=b。
∵AC=AD+CD,AC=a,AD=b,
∴CD=AC-AD=a-b。
a - b
16. 对于实数a,b,定义一种新运算“$\otimes $”:$a\otimes b= \frac {1}{a-b^{2}}$,这里等号的右边是实数运算.例如:$1\otimes 3= \frac {1}{1-3^{2}}= -\frac {1}{8}$,则方程$x\otimes (-2)= \frac {2}{x-4}-1$的解是______
x = 5
.
答案:x = 5
解析:
解:由新运算定义可得,$x\otimes (-2)=\frac{1}{x - (-2)^2}=\frac{1}{x - 4}$。
已知$x\otimes (-2)=\frac{2}{x - 4}-1$,则$\frac{1}{x - 4}=\frac{2}{x - 4}-1$。
方程两边同乘$x - 4$得:$1 = 2 - (x - 4)$。
去括号:$1 = 2 - x + 4$。
移项、合并同类项:$x = 2 + 4 - 1$,解得$x = 5$。
检验:当$x = 5$时,$x - 4 = 5 - 4 = 1\neq 0$,所以$x = 5$是原方程的解。
答案:$x = 5$
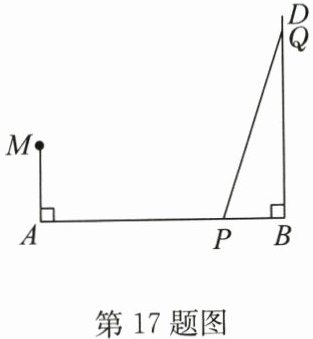
17. 如图,已知线段$AB= 20m,MA⊥AB$于点A,$MA= 6m$,射线$BD⊥AB$于点B,点P从点B向点A运动,每秒走1m,点Q从点B向点D运动,每秒走3m.若点P,Q同时从点B出发,则出发
5
s后,在线段MA上有一点C,使$△CAP与△PBQ$全等.
答案:5
解析:
解:设出发 $ t $ 秒后,$\triangle CAP$ 与 $\triangle PBQ$ 全等。
由题意得:$ BP = t \, \text{m} $,$ BQ = 3t \, \text{m} $,$ AP = AB - BP = (20 - t) \, \text{m} $。
因为 $ MA \perp AB $,$ BD \perp AB $,所以 $\angle A = \angle B = 90^\circ$。
分两种情况讨论:
情况1: 若 $\triangle CAP \cong \triangle PBQ$,则 $ AC = BP $,$ AP = BQ $。
$\begin{cases}AC = t \\20 - t = 3t\end{cases}$
解得 $ t = 5 $,此时 $ AC = 5 \, \text{m} $,因为 $ MA = 6 \, \text{m} $,$ 5 < 6 $,点 $ C $ 在线段 $ MA $ 上,符合题意。
情况2: 若 $\triangle CAP \cong \triangle QBP$,则 $ AC = BQ $,$ AP = BP $。
$\begin{cases}AC = 3t \\20 - t = t\end{cases}$
解得 $ t = 10 $,此时 $ AC = 30 \, \text{m} $,因为 $ MA = 6 \, \text{m} $,$ 30 > 6 $,点 $ C $ 不在线段 $ MA $ 上,不符合题意,舍去。
综上,出发 $ 5 $ 秒后满足条件。
$5$
18. 已知$abc≠0,\frac {a+b-c}{c}= \frac {a-b+c}{b}= \frac {-a+b+c}{a}$,则$\frac {(a+b)(b+c)(c+a)}{abc}$的值是
8 或 -1
.
答案:8 或 -1
解析:
设$\frac{a+b - c}{c}=\frac{a - b + c}{b}=\frac{-a + b + c}{a}=k$,则有:
$a + b - c = kc$,即$a + b=(k + 1)c$;
$a - b + c = kb$,即$a + c=(k + 1)b$;
$-a + b + c = ka$,即$b + c=(k + 1)a$。
将上述三式相加得:$2(a + b + c)=(k + 1)(a + b + c)$。
情况一:当$a + b + c≠0$时,$k + 1=2$,即$k = 1$。
此时$a + b=2c$,$a + c=2b$,$b + c=2a$,
$\frac{(a + b)(b + c)(c + a)}{abc}=\frac{2c\cdot2a\cdot2b}{abc}=8$。
情况二:当$a + b + c=0$时,$a + b=-c$,$b + c=-a$,$c + a=-b$,
$\frac{(a + b)(b + c)(c + a)}{abc}=\frac{(-c)(-a)(-b)}{abc}=-1$。
综上,$\frac{(a + b)(b + c)(c + a)}{abc}$的值是$8$或$-1$。
答案:$8$或$-1$