2025年启东中学作业本八年级数学上册人教版第170页解析答案

23. (10分)(1)$99^{2}-1$能否被100整除？
(2)n为整数,$(2n + 1)^{2}-25$能否被4整除？

答案：(1)因为 $99^2 - 1 = (99 + 1)(99 - 1) = 100×98$，
所以 $99^2 - 1$ 能被 100 整除。
(2)原式 $= (2n + 1 + 5)(2n + 1 - 5) = (2n + 6)(2n - 4) = 2(n + 3)×2(n - 2) = 4(n + 3)(n - 2)$。
因为 $n$ 为整数，所以 $n + 3$ 和 $n - 2$ 都为整数，
所以 $(2n + 1)^2 - 25$ 能被 4 整除。

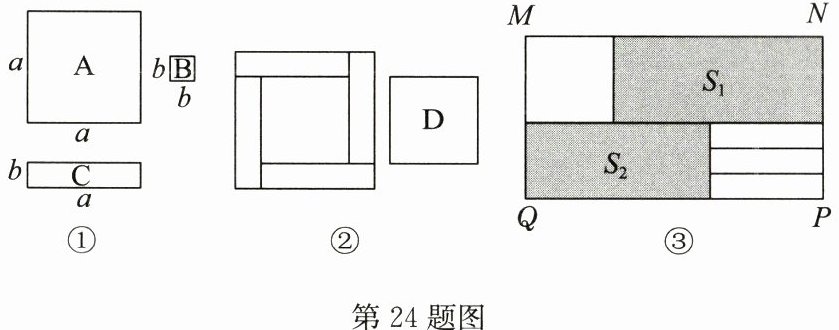
24. (10分)(2024春·秦汇区月考)老师拿出三种型号的卡片,如图①.
(1)利用多项式与多项式相乘的法则,计算：$(a + 2b)(a + b)= $

$a^2 + 3ab + 2b^2$

；
(2)选取1张A型卡片,4张C型卡片,则应取

张B型卡片才能用它们拼成一个新的正方形,这个新的正方形的边长是

$a + 2b$

(用含a,b的代数式表示)；
(3)选取4张C型卡片在纸上按图②的方式拼图,并剪出中间的正方形作为第四种D型卡片,由此可检验的等量关系为

$(a + b)^2 - 4ab = (a - b)^2$

；
(4)选取1张D型卡片,3张C型卡片按图③的方式不重叠地放在长方形MNPQ框架内,已知NP的长度固定不变,MN的长度可以变化,且$MN ＞ a$,图中两阴影部分(长方形)的面积分别表示为$S_{1}$,$S_{2}$,若$S_{1}-S_{2}= 3b^{2}$,则a与b之间有什么数量关系？请说明理由.

解：$a$ 与 $b$ 之间的数量关系为 $a = 4b$。理由如下：
设 $MN = x$。
根据题意，得 $S_1 = (a - b)(x - a + b) = ax - bx - a^2 + 2ab - b^2$，$S_2 = 3b(x - a) = 3bx - 3ab$。
$\because S_1 - S_2 = 3b^2$，
$\therefore ax - bx - a^2 + 2ab - b^2 - (3bx - 3ab) = 3b^2$，
$\therefore (a - 4b)x - a^2 + 5ab - b^2 = 3b^2$，
$\therefore (a - 4b)x - (a^2 - 5ab + 4b^2) = 0$，
$\therefore (a - 4b)x - (a - 4b)(a - b) = 0$，
$\therefore (a - 4b)[x - (a - b)] = 0$，
$\therefore (x - a + b)(a - 4b) = 0$。
$\because x ＞ a$，$\therefore a - 4b = 0$，$\therefore a = 4b$，
$\therefore a$ 与 $b$ 之间的数量关系为 $a = 4b$。

答案：(1)$a^2 + 3ab + 2b^2$
(2)4 $a + 2b$
(3)$(a + b)^2 - 4ab = (a - b)^2$
(4)解：$a$ 与 $b$ 之间的数量关系为 $a = 4b$。理由如下：
设 $MN = x$。
根据题意，得 $S_1 = (a - b)(x - a + b) = ax - bx - a^2 + 2ab - b^2$，$S_2 = 3b(x - a) = 3bx - 3ab$。
$\because S_1 - S_2 = 3b^2$，
$\therefore ax - bx - a^2 + 2ab - b^2 - (3bx - 3ab) = 3b^2$，
$\therefore (a - 4b)x - a^2 + 5ab - b^2 = 3b^2$，
$\therefore (a - 4b)x - (a^2 - 5ab + 4b^2) = 0$，
$\therefore (a - 4b)x - (a - 4b)(a - b) = 0$，
$\therefore (a - 4b)[x - (a - b)] = 0$，
$\therefore (x - a + b)(a - 4b) = 0$。
$\because x ＞ a$，$\therefore a - 4b = 0$，$\therefore a = 4b$，
$\therefore a$ 与 $b$ 之间的数量关系为 $a = 4b$。