6. (2023·淮安淮阴期中)如图,C是线段BG上的一点,以BC,CG为边向两A
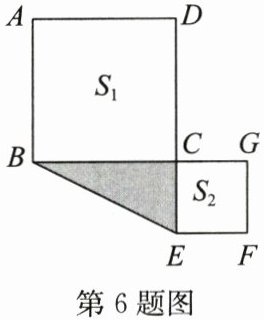
边作正方形,面积分别是$S_{1}和S_{2}$,两个正方形的面积和$S_{1}+S_{2}= 20$,已知BG= 6,则图中阴影部分的面积为(
A
)
A.4
B.6
C.7
D.8
解析:
设正方形$ABCD$的边长为$a$,正方形$CEFG$的边长为$b$。
因为$S_{1}$和$S_{2}$分别是两个正方形的面积,所以$S_{1}=a^{2}$,$S_{2}=b^{2}$。已知$S_{1}+S_{2}=20$,则$a^{2}+b^{2}=20$。
又因为$BG=6$,且$BG=BC + CG=a + b$,所以$a + b=6$。
对$(a + b)^{2}$进行展开可得$(a + b)^{2}=a^{2}+2ab + b^{2}$,将$a + b=6$,$a^{2}+b^{2}=20$代入可得:
$6^{2}=20 + 2ab$
$36=20 + 2ab$
$2ab=36 - 20$
$2ab=16$
$ab=8$
由图可知,阴影部分是一个三角形,其底为$a$,高为$b$,所以阴影部分的面积为$\frac{1}{2}ab$。
将$ab=8$代入可得:$\frac{1}{2}×8 = 4$。
故答案为A。