9. 如图,在$\triangle ABC$中,$AB = AC = 6$,该三角形的面积为15,$O是边BC$上任意一点,则点$O到边AB$,$AC$的距离之和等于(
A
)
A.5
B.7.5
C.9
D.10
答案:1. 首先,连接$AO$:
设$O$到$AB$的距离为$h_1$(即$OE = h_1$),$O$到$AC$的距离为$h_2$(即$OF = h_2$)。
根据三角形面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),$\triangle ABC$的面积$S_{\triangle ABC}=S_{\triangle ABO}+S_{\triangle ACO}$。
已知$AB = AC = 6$,$S_{\triangle ABO}=\frac{1}{2}AB× OE$,$S_{\triangle ACO}=\frac{1}{2}AC× OF$。
2. 然后,代入面积公式:
因为$S_{\triangle ABC}=15$,$AB = AC = 6$,$S_{\triangle ABC}=\frac{1}{2}AB× OE+\frac{1}{2}AC× OF$。
把$AB = AC = 6$代入上式得$S_{\triangle ABC}=\frac{1}{2}× AB×(OE + OF)$(因为$AB = AC$)。
已知$S_{\triangle ABC}=15$,$AB = 6$,根据$S=\frac{1}{2}ah$(这里$a = AB$,$h=OE + OF$),则$15=\frac{1}{2}×6×(OE + OF)$。
3. 最后,求解$OE + OF$:
由$15=\frac{1}{2}×6×(OE + OF)$,化简方程$15 = 3×(OE + OF)$。
两边同时除以$3$,可得$OE + OF=\frac{15}{3}=5$。
所以点$O$到边$AB$,$AC$的距离之和等于$5$,答案是A。
解析:
解:连接AO,设点O到AB的距离为h₁,到AC的距离为h₂。
∵AB=AC=6,S△ABC=15,
∴S△ABC=S△ABO+S△ACO,
即15=1/2×AB×h₁ + 1/2×AC×h₂。
∵AB=AC=6,
∴15=1/2×6×h₁ + 1/2×6×h₂=3(h₁+h₂),
∴h₁+h₂=5。
答案:A
10. 如图,在$\triangle ABC$中,$AD平分\angle BAC$,交$BC于点D$,$M$,$N分别是AD和AB$上的动点,$AB = 8$,$\angle BAC = 60^{\circ}$,当$BM + MN$的值最小时,$BN$的长为(
C
)
A.2
B.3
C.4
D.5
答案:1. 首先,作$B$关于$AD$的对称点$B'$:
因为$AD$平分$\angle BAC$,所以$B'$在$AC$上,且$AB = AB'$,$BM=B'M$。
则$BM + MN=B'M + MN$。
根据“两点之间,线段最短”,当$B'$,$M$,$N$三点共线且$B'N\perp AB$时,$BM + MN = B'N$的值最小。
2. 然后,已知$\angle BAC = 60^{\circ}$,$AB = AB'=8$:
在$Rt\triangle AB'N$中,$\angle ANB' = 90^{\circ}$,$\angle B'AN = 60^{\circ}$,$\angle AB'N = 30^{\circ}$。
根据直角三角形中$30^{\circ}$所对的直角边等于斜边的一半的性质,在$Rt\triangle AB'N$中,设$AN=x$,则$AB' = 2x$($AB'$为斜边,$AN$为$30^{\circ}$角$\angle AB'N$所对的直角边)。
又因为$AB'=8$,所以$2x = 8$,解得$x = 4$。
那么$BN=AB - AN$。
已知$AB = 8$,$AN = 4$,所以$BN=8 - 4=4$。
所以当$BM + MN$的值最小时,$BN$的长为$4$,答案是C。
解析:
解:作点B关于AD的对称点B',过点B'作B'N⊥AB于点N,交AD于点M,此时BM+MN的值最小。
∵AD平分∠BAC,∠BAC=60°,
∴∠BAD=30°。
∵点B与B'关于AD对称,
∴AD垂直平分BB',∠B'AD=∠BAD=30°,AB'=AB=8。
∴∠B'AB=∠B'AD+∠BAD=60°。
∵B'N⊥AB,
∴∠ANB'=90°,
∴△AB'N是直角三角形。
在Rt△AB'N中,∠B'AN=60°,AB'=8,
∴AN=AB'·cos60°=8×1/2=4。
∵AB=8,
∴BN=AB-AN=8-4=4。
答案:C
11. 小明照镜子时,发现衣服上的英文字母在镜子中呈现为“$\exists \text{J}99\text{A}$”,则这组英文字母是
APPLE
。
答案:APPLE
12. 在等腰三角形、等边三角形、非等腰直角三角形、等腰直角三角形中,轴对称图形有
3
个。
答案:3
解析:
解:等腰三角形是轴对称图形,有1条对称轴;
等边三角形是轴对称图形,有3条对称轴;
非等腰直角三角形不是轴对称图形;
等腰直角三角形是轴对称图形,有1条对称轴。
轴对称图形有3个。
答案:3
13. 设$a$,$b$分别是等腰三角形的两条边的长,$m$是这个三角形的周长,当$a$,$b$,$m满足方程组\begin{cases}a - 2b = m - 7,\\a + b= \frac{m}{4}+2\end{cases} $时,$m$的值是
5或$\frac{16}{3}$
。
答案:5或$\frac{16}{3}$
14. 如图,在$\triangle ABC$中,$BC边的垂直平分线交BC于点D$,交$AB于点E$,连接$CE$。若$CE平分\angle ACB$,$\angle B = 42^{\circ}$,则$\angle A = $
54
$^{\circ}$。
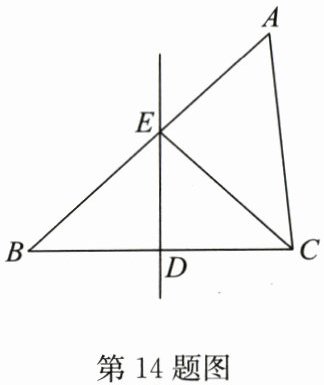
答案:54
解析:
解:
∵DE是BC的垂直平分线,
∴EB=EC,
∴∠ECB=∠B=42°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=84°,
∵在△ABC中,∠A+∠B+∠ACB=180°,
∴∠A=180°-∠B-∠ACB=180°-42°-84°=54°。
54
15. 在平面直角坐标系$xOy$中,已知$A(2,-2)$,在坐标轴上确定一点$B$,使$\triangle AOB$为等腰三角形,则符合条件的点$B$有
8
个。
答案:8
解析:
解:已知点$A(2,-2)$,$O$为坐标原点$(0,0)$。
情况一:以$O$为顶点,$OA$为腰
$OA=\sqrt{(2-0)^2+(-2-0)^2}=\sqrt{8}=2\sqrt{2}$
在$x$轴上:$B_1(2\sqrt{2},0)$,$B_2(-2\sqrt{2},0)$
在$y$轴上:$B_3(0,2\sqrt{2})$,$B_4(0,-2\sqrt{2})$
情况二:以$A$为顶点,$OA$为腰
在$x$轴上:设$B(x,0)$,$(x-2)^2+(0+2)^2=(2\sqrt{2})^2$,解得$x=4$($x=0$与$O$重合,舍去),即$B_5(4,0)$
在$y$轴上:设$B(0,y)$,$(0-2)^2+(y+2)^2=(2\sqrt{2})^2$,解得$y=-4$($y=0$与$O$重合,舍去),即$B_6(0,-4)$
情况三:以$OA$为底边
在$x$轴上:设$B(x,0)$,$OA$中垂线方程为$y=x$,与$x$轴交于$B_7(0,0)$(与$O$重合,舍去),另解:$x^2=(x-2)^2+4$,解得$x=2$,即$B_7(2,0)$
在$y$轴上:设$B(0,y)$,$y^2=4+(y+2)^2$,解得$y=-2$,即$B_8(0,-2)$
综上,符合条件的点$B$有$8$个。
答案:$8$
16. 如图,在三角形纸片$ABC$中,$AC = BC$。把$\triangle ABC沿着AC$翻折,点$B落在点D$处,连接$BD$。若$\angle BAC = 40^{\circ}$,则$\angle CBD$的度数是
10°
。
答案:10°
17. 如图,在四边形$ABCD$中,$AC = BC$,$\angle ACB= \angle ADC = 90^{\circ}$,$CD = 20$,则$\triangle BCD$的面积为______。

200
答案:200
解析:
解:过点$B$作$BE \perp CD$,交$DC$的延长线于点$E$。
$\because \angle ACB = 90^{\circ}$,$\angle ADC = 90^{\circ}$,
$\therefore \angle ACD + \angle BCE = 90^{\circ}$,$\angle ACD + \angle CAD = 90^{\circ}$,
$\therefore \angle BCE = \angle CAD$。
在$\triangle ACD$和$\triangle CBE$中,
$\begin{cases} \angle ADC = \angle CEB = 90^{\circ} \\\angle CAD = \angle BCE \\AC = CB \end{cases}$,
$\therefore \triangle ACD \cong \triangle CBE(AAS)$,
$\therefore BE = CD = 20$。
$\therefore S_{\triangle BCD} = \frac{1}{2} × CD × BE = \frac{1}{2} × 20 × 20 = 200$。
200