11. (2024春·建湖县期中)【定义】如果两个角的差为$36^{\circ }$,就称这两个角互为“黄金角”,其中一个角叫作另一个角的“黄金角”.
例如:$α=76^{\circ },β=40^{\circ },α-β= 36^{\circ }$,则α和β互为“黄金角”,即α是β的“黄金角”,β也是α的“黄金角”.
(1)已知$∠1和∠2$互为“黄金角”,且$∠1>∠2$,若$∠1和∠2$互余,则$∠1=$
63°
.
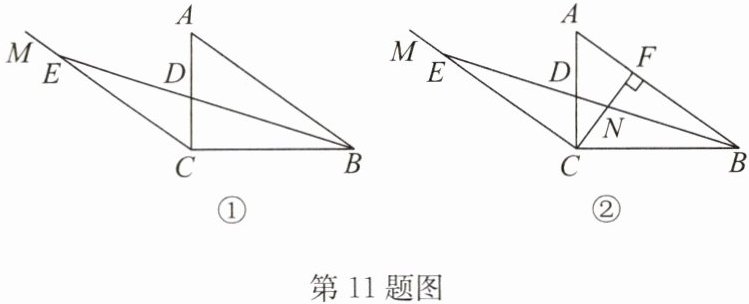
(2)如图①,在$△ABC$中,$∠ACB= 90^{\circ }$,过点C作AB的平行线CM,$∠ABC$的平分线分别交AC,CM于D,E两点.
①若$∠A>∠BEC$,且$∠A和∠BEC$互为“黄金角”,则$∠A=$
54°
;
②如图②,过点C作AB的垂线,垂足为F,BD与CF相交于点N.若$∠DCN与∠CDN$互为“黄金角”,求$∠A$的度数.
解:设∠DCN=x.
∵∠DCN与∠CDN互为“黄金角”,
∴∠CDN=x+36°或∠CDN=x-36°.
当∠CDN=x+36°时,
∵∠ACB=90°,
∴∠CBN=90°-∠CDN
=90°-(x+36°)
=54°-x.
∵BE平分∠ABC,
∴∠ABC=2∠CBD=108°-2x.
∵CF⊥AB,
∴∠A=90°-∠DCN=90°-x.
∵∠A+∠ABC=90°,
∴90°-x+108°-2x=90°,
解得x=36°,
∴∠A=90°-36°=54°.
当∠CDN=x-36°时,
∵∠ACB=90°,
∴∠CBD=90°-∠CDN
=90°-(x-36°)
=126°-x.
∵BE平分∠ABC,
∴∠ABC=2∠CBN=252°-2x.
∵CF⊥AB,
∴∠A=90°-∠DCN=90°-x.
∵∠A+∠ABC=90°,
∴90°-x+252°-2x=90°,
解得x=84°,
∴∠A=90°-84°=6°.
综上所述,∠A=54°或∠A=6°.