1. (2024·浙江模拟)将一副直角三角板按如图所示方式摆放,若$AB//EF$,则$∠1= $
D
A.$45^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$
答案:D
解析:
由题意知,一副直角三角板中,含$30^\circ$角的三角板各角为$30^\circ$、$60^\circ$、$90^\circ$,含$45^\circ$角的三角板各角为$45^\circ$、$45^\circ$、$90^\circ$。
设$AB$与$EF$的交点为$G$,$AB//EF$,则$\angle AGF = \angle ABE$(两直线平行,内错角相等)。
在含$45^\circ$角的三角板中,$\angle ABE = 45^\circ$,故$\angle AGF = 45^\circ$。
在含$30^\circ$角的三角板中,$\angle BAC = 30^\circ$,$\angle 1$为$\triangle AGF$的外角,所以$\angle 1 = \angle BAC + \angle AGF = 30^\circ + 45^\circ = 75^\circ$。
D
2. 如图,$\triangle ABC$中,$AD$,$BE分别是\triangle ABC$的高和角平分线,若$∠C= 70^{\circ}$,$∠AEB= 95^{\circ}$,则$∠BAD= $
40
$^{\circ}$。
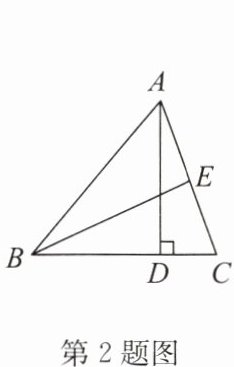
答案:40
解析:
在$\triangle ABC$中,$BE$是角平分线,设$\angle ABE = \angle EBC = x$。
在$\triangle BEC$中,$\angle C = 70^\circ$,$\angle AEB = 95^\circ$,则$\angle BEC = 180^\circ - 95^\circ = 85^\circ$。
因为$\angle EBC + \angle C + \angle BEC = 180^\circ$,所以$x + 70^\circ + 85^\circ = 180^\circ$,解得$x = 25^\circ$,故$\angle ABC = 2x = 50^\circ$。
在$\triangle ABC$中,$\angle BAC = 180^\circ - \angle ABC - \angle C = 180^\circ - 50^\circ - 70^\circ = 60^\circ$。
因为$AD$是高,所以$\angle ADC = 90^\circ$,在$\triangle ADC$中,$\angle DAC = 180^\circ - 90^\circ - 70^\circ = 20^\circ$。
则$\angle BAD = \angle BAC - \angle DAC = 60^\circ - 20^\circ = 40^\circ$。
$40$
3. 在$\triangle ABC$中,$∠A= 60^{\circ}$,高$BE$,$CF所在的直线相交于点O$,且点$O不与点B$,$C$重合,则$∠BOC= $
60或120
$^{\circ}$。
答案:60或120
解析:
当$\triangle ABC$为锐角三角形时,
$\because BE$,$CF$为高,
$\therefore \angle AEB=\angle AFC=90^{\circ}$,
$\because \angle A=60^{\circ}$,
$\therefore \angle EOF=360^{\circ}-90^{\circ}-90^{\circ}-60^{\circ}=120^{\circ}$,
$\because \angle BOC=\angle EOF$,
$\therefore \angle BOC=120^{\circ}$;
当$\triangle ABC$为钝角三角形时,
不妨设$\angle B$为钝角,
$\because BE$,$CF$为高,
$\therefore \angle OEC=\angle OFB=90^{\circ}$,
$\because \angle A=60^{\circ}$,
$\therefore \angle ACF=30^{\circ}$,
$\therefore \angle BOC=90^{\circ}-30^{\circ}=60^{\circ}$。
综上,$\angle BOC=60^{\circ}$或$120^{\circ}$。
$60$或$120$
4. 如图,在$\triangle ABC$中,$∠1= ∠2= ∠3$。
(1)证明:$∠BAC= ∠DEF$;
(2)若$∠BAC= 70^{\circ}$,$∠DFE= 50^{\circ}$,求$∠ABC$的度数。

答案:
(1)证明:
∵∠BAC=∠1+∠CAE,∠DEF=∠3+∠CAE,∠1=∠3,
∴∠BAC=∠DEF.
(2)解:
∵∠ABC=∠2+∠ABD,∠1=∠2,
∴∠ABC=∠1+∠ABD=∠EDF.
由
(1)可知∠DEF=∠BAC=70°,
∴∠ABC=∠1+∠ABD=∠EDF=180°-∠DEF-∠DFE=180°-70°-50°=60°,
∴∠ABC=60°.
5. (2024春·姜堰区月考)如图,$∠ABD$,$∠ACD的平分线交于点P$,若$∠A= 50^{\circ}$,$∠D= 10^{\circ}$,则$∠P$的度数为(
B
)
A.$15^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
答案:B
解析:
连接BC,设∠ABD=2α,∠ACD=2β。
在△ABC中,∠ABC+∠ACB=180°-∠A=130°。
在△DBC中,∠DBC+∠DCB=180°-∠D=170°。
∠DBC+∠DCB=(∠ABC+∠ABD)+(∠ACB-∠ACD)=∠ABC+∠ACB+2α-2β=130°+2α-2β=170°,得α-β=20°。
在△PBC中,∠PBC+∠PCB=∠ABC+α+∠ACB-β=130°+(α-β)=150°。
∠P=180°-(∠PBC+∠PCB)=30°。
答案:D
6. 如图,$BE是\triangle ABC的外角∠CBD$的平分线,且$BE交AC的延长线于点E$。若$∠A= 30^{\circ}$,$∠E= 20^{\circ}$,则$∠ACB$的度数是(
C
)

A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:C
解析:
在$\triangle ABE$中,$\angle A=30^{\circ}$,$\angle E=20^{\circ}$,根据三角形内角和定理,$\angle ABE=180^{\circ}-\angle A-\angle E=180^{\circ}-30^{\circ}-20^{\circ}=130^{\circ}$。
因为$BE$是$\angle CBD$的平分线,所以$\angle CBE=\angle EBD$。
又因为$\angle ABE+\angle EBD=180^{\circ}$,所以$\angle EBD=180^{\circ}-\angle ABE=180^{\circ}-130^{\circ}=50^{\circ}$,故$\angle CBE=50^{\circ}$。
在$\triangle BCE$中,$\angle E=20^{\circ}$,$\angle CBE=50^{\circ}$,根据三角形内角和定理,$\angle BCE=180^{\circ}-\angle E-\angle CBE=180^{\circ}-20^{\circ}-50^{\circ}=110^{\circ}$。
因为$\angle ACB+\angle BCE=180^{\circ}$,所以$\angle ACB=180^{\circ}-\angle BCE=180^{\circ}-110^{\circ}=70^{\circ}$。
C