1. 在一个直角三角形中,一个锐角是$40^{\circ }$,另一个锐角是 (
B
)
A.$70^{\circ }$
B.$50^{\circ }$
C.$30^{\circ }$
D.$10^{\circ }$
答案:B
解析:
直角三角形两锐角和为$90^{\circ }$,另一个锐角为$90^{\circ } - 40^{\circ } = 50^{\circ }$
B
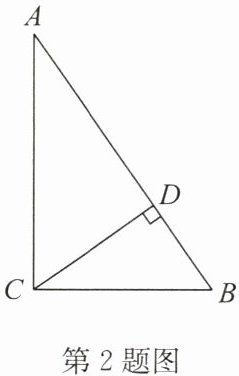
2. (2024秋·阳泉期中)如图,在$Rt△ABC$中,$∠ACB= 90^{\circ },CD⊥AB$于点D.若$∠A= 35^{\circ }$,则$∠BCD$的度数为 (
B
)
A.$40^{\circ }$
B.$35^{\circ }$
C.$30^{\circ }$
D.$25^{\circ }$
答案:B
解析:
在$Rt\triangle ABC$中,$\angle ACB=90^{\circ}$,$\angle A=35^{\circ}$,
$\therefore \angle B=90^{\circ}-\angle A=90^{\circ}-35^{\circ}=55^{\circ}$。
$\because CD\perp AB$,
$\therefore \angle CDB=90^{\circ}$。
在$Rt\triangle CDB$中,$\angle BCD=90^{\circ}-\angle B=90^{\circ}-55^{\circ}=35^{\circ}$。
B
3. (2023春·南京期末)直角三角形中两个锐角的差为$20^{\circ }$,则较小的锐角度数是
35
$^{\circ }$.
答案:35
解析:
设较小的锐角度数为$x$,则另一个锐角度数为$x + 20^{\circ}$。
因为直角三角形的两个锐角和为$90^{\circ}$,所以可得方程:
$x + (x + 20^{\circ}) = 90^{\circ}$
$2x + 20^{\circ} = 90^{\circ}$
$2x = 90^{\circ} - 20^{\circ}$
$2x = 70^{\circ}$
$x = 35^{\circ}$
35
4. 如图,在$Rt△ABC$中,$∠ACB= 90^{\circ }$,CD是边AB上的高,$∠1= 32^{\circ }$,求$∠2,∠B,∠A$的度数.

答案:解:在Rt△ABC中,∠ACB=90°,∠1=32°,
∴∠2=90°-∠1=90°-32°=58°.
∵CD是边AB上的高,
∴∠BDC=∠ADC=90°,
∴∠A=90°-∠1=90°-32°=58°,∠B=90°-∠2=90°-58°=32°.
5. 具备下列条件的$△ABC$中,不是直角三角形的是 (
D
)
A.$∠A+∠B= ∠C$
B.$∠A-∠B= ∠C$
C.$∠A:∠B:∠C= 1:2:3$
D.$∠A= ∠B= 3∠C$
答案:D
解析:
A.
∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=90°,是直角三角形;
B.
∵∠A-∠B=∠C,∠A+∠B+∠C=180°,
∴∠A=90°,是直角三角形;
C.
∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠C=180°×$\frac{3}{1+2+3}$=90°,是直角三角形;
D.
∵∠A=∠B=3∠C,∠A+∠B+∠C=180°,
∴3∠C+3∠C+∠C=180°,∠C=$\frac{180°}{7}$,∠A=∠B=$\frac{540°}{7}$≠90°,不是直角三角形。
D
6. 如图,$△ABC与△CDE$均为直角三角形,AB交CD于点F,$∠ACB= ∠CDE= 90^{\circ },∠B= 30^{\circ },∠E= 45^{\circ },∠ECB= α$,则$∠CFB= $ (
C
)

A.$α+90^{\circ }$
B.$α+45^{\circ }$
C.$105^{\circ }-α$
D.$180^{\circ }-α$
答案:C
解析:
在$△ABC$中,$∠ACB=90^{\circ}$,$∠B=30^{\circ}$,则$∠A=180^{\circ}-∠ACB-∠B=60^{\circ}$。
在$△CDE$中,$∠CDE=90^{\circ}$,$∠E=45^{\circ}$,则$∠DCE=180^{\circ}-∠CDE-∠E=45^{\circ}$。
因为$∠ECB=α$,$∠ACB=90^{\circ}$,所以$∠ACF=∠ACB - ∠ECB - ∠DCE=90^{\circ}-α - 45^{\circ}=45^{\circ}-α$。
在$△AFC$中,$∠AFC=180^{\circ}-∠A - ∠ACF=180^{\circ}-60^{\circ}-(45^{\circ}-α)=75^{\circ}+α$。
因为$∠AFC$与$∠CFB$互补,所以$∠CFB=180^{\circ}-∠AFC=180^{\circ}-(75^{\circ}+α)=105^{\circ}-α$。
C
7. 有一道题:“如图,在$△ABC$中,$∠C= 90^{\circ }$,将$△ABC$沿DE折叠,使得点B落在边AC上的点F处,若$∠CFD= 60^{\circ }$,且$△AEF$中有两个内角相等,求$∠A$的度数.”嘉嘉的答案是$∠A= 40^{\circ }$,淇淇说:“嘉嘉考虑得不全而,$∠A$还应该有另外一个值.”下列判断正确的是 (
B
)

A.淇淇说得不对,$∠A就是40^{\circ }$
B.淇淇说得对,且$∠A的另一个值是50^{\circ }$
C.淇淇说得对,且$∠A的另一个值是55^{\circ }$
D.两人都不对,$∠A$应有三个不同值
答案:B
解析:
设∠A=x,∠B=90°-x。
由折叠得∠DFE=∠B=90°-x,∠FDE=∠BDE,∠FED=∠BED。
∵∠CFD=60°,∠C=90°,
∴∠CDF=30°,∠FDB=150°,∠FDE=∠BDE=75°。
情况1:∠AEF=∠AFE
∠AFD=180°-∠CFD=120°,∠AFE=∠AFD-∠DFE=120°-(90°-x)=30°+x。
∠AEF=∠AFE=30°+x。
在△AEF中,∠A+∠AEF+∠AFE=180°,x+2(30°+x)=180°,解得x=40°。
情况2:∠A=∠AEF
∠AFE=180°-2x。
∠AFE=∠AFD-∠DFE=30°+x,
∴180°-2x=30°+x,解得x=50°。
情况3:∠A=∠AFE
∠AFE=x,∠AFE=30°+x,x=30°+x,无解。
综上,∠A=40°或50°。
答案:B
8. 在直角三角形ABC中,$∠A:∠B:∠C= 2:m:4$,则m的值是____
2或6
.
答案:2或6
解析:
∵∠A:∠B:∠C=2:m:4,
∴设∠A=2k,∠B=mk,∠C=4k(k>0)。
∵三角形ABC是直角三角形,
∴分三种情况:
情况1:∠A=90°,则2k=90°,k=45°,∠C=4k=180°,不符合三角形内角和定理,舍去;
情况2:∠B=90°,则mk=90°,2k+mk+4k=180°,即6k+90°=180°,k=15°,m=6;
情况3:∠C=90°,则4k=90°,k=22.5°,∠A=2k=45°,∠B=mk=180°-90°-45°=45°,mk=45°,m=2。
综上,m的值是2或6。