2. 阅读教材第 94 页“综合与实践”,解决下列问题:
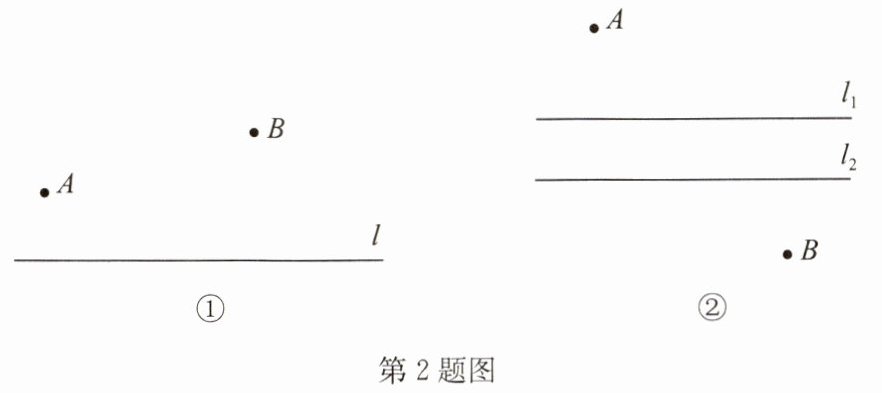
(1)如图①,直线$l同侧有A$,$B$两个公园,某施工队要在直线$l上建一个材料供应点P$,使得从$A公园经P点到B$公园的路径最短.
①请在图①中画出点$P$的位置,并详细说明作图依据;
②若在直线$l上选取另一点Q$(点$Q与点P$不重合),试通过说理的方式证明$AP+PB<AQ+QB$.
(2)如图②,$A$,$B$是两条平行街道(街道宽度忽略不计)两侧的两个小区,现在要在两条街道上分别设取件点$N$,$M$,使得$A小区居民经N到M再到B$小区的路径最短. 请画出$M$,$N$的位置,并阐述作图思路.
答案:2.解:
(1)①如答图①,作点A关于直线l的对称点A',连接A'B,与直线l的交点即为点P.
依据:因为点A与A'关于直线l对称,所以直线l是线段AA'的垂直平分线.根据垂直平分线的性质,垂直平分线上的点到线段两端的距离相等,即PA=PA',那么AP+PB=A'P+PB,又因为两点之间线段最短,所以A'B最短,即此时AP+PB最小.

②如答图②,连接A'Q.
因为点A与A'关于直线l对称,所以AQ=A'Q.
在△A'QB中,根据三角形三边关系“两边之和大于第三边”,可得A'P+PB<A'Q+QB.
因为AP=A'P,AQ=A'Q,所以AP+PB<AQ+QB.

(2)如答图③,将点A沿垂直于街道的方向平移,平移距离为两条街道间的距离,得到点A',连接A'B,与街道l₂交于点M,过点M作街道l₂的垂线,与街道l₁交于点N.
在AN+MN+MB中,MN是街道宽度,为定值,当AN+BM值最小时,路径最短.根据“两点之间,线段最短”知,A'M+MB最短,又AN=A'M,所以AN+MN+MB最短.
