1. 阅读教材第 86 页“探究与发现”,解决下列问题:
在初中数学综合与实践课上,老师带领同学们探究三角形中边与角之间的不等关系.
【探究过程回顾】
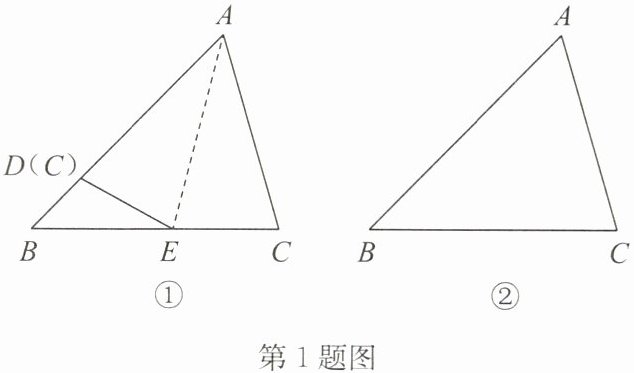
如图①,在$\triangle ABC$中,若$AB>AC$,将$\triangle ABC$折叠,使边$AC落在AB$上,点$C落在AB上的D$点,折痕交$BC于点E$,可得$∠C= ∠ADE$,且$∠ADE>∠B$,所以$∠C>∠B$,即证明了在一个三角形中,大边所对的角较大.
【新的探究任务】
(1)请仿照上述方法,借助图②说明“在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大”;
(2)在$\triangle ABC$中,已知$BC= 8$,$AB= 5$,$AC= 6$,请判断$∠A$,$∠B$,$∠C$的大小关系,并说明理由;
(3)在$\triangle DEF$中,已知$∠D= 30^{\circ}$,$∠E= 60^{\circ}$,$∠F= 90^{\circ}$,请指出三边$DE$,$EF$,$DF$的大小关系,并说明理由.
答案:1.解:
(1)设在△ABC中,∠C>∠B.
如答图,在∠C内部作∠BCD=∠B,CD交AB于点D.根据等角对等边,可得BD=CD.
在△ACD中,AD+CD>AC;
因为BD=CD,AB=AD+BD,所以AB>AC.
即证明了在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大.

(2)因为BC=8,AB=5,AC=6,且BC>AC>AB,
所以∠A>∠B>∠C;
(3)因为∠F=90°,∠E=60°,∠D=30°,且∠F>∠E>∠D,所以DE>DF>EF.