4. 已知$\triangle ACD和\triangle BCE$都是等腰直角三角形,$\angle ACD = \angle BCE = 90^{\circ}$。
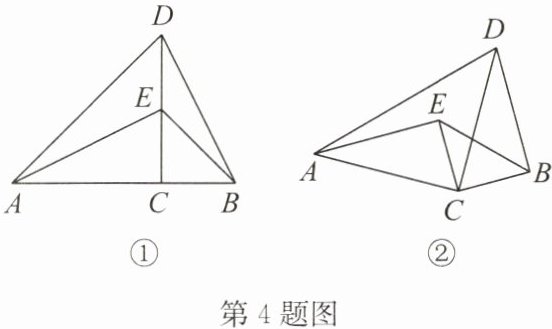
【初步探索】(1) 如图①,摆放$\triangle ACD和\triangle BCE$(点$A$,$C$,$B$在同一条直线上,点$E在CD$上),连接$AE$,$BD$,判断线段$AE与BD$的数量关系和位置关系;
【拓展延伸】(2) 如图②,摆放$\triangle ACD和\triangle BCE$,连接$AE$,$BD$,(1) 中的结论是否仍然成立?请说明理由。

答案:4.解:
(1)如答图①,延长AE交BD于点F.
在△ACE和△DCB中,{AC=DC,
∠ACE=∠DCB,
CE=CB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAE=∠CDB.
∵∠CDB+∠DBC=90°,
∴∠CAE+∠DBC=90°,
∴∠AFB=90°,
∴AE⊥BD.
(2)
(1)中的结论仍然成立,AE=BD,AE⊥BD.理由如下:
如答图②,延长AE交BD于点M,交CD于点G.
∵∠ACD=∠BCE=90°,
∴∠ACD−∠ECD=∠BCE−∠ECD,即∠ACE=∠DCB.
在△ACE和△DCB中,{AC=DC,
∠ACE=∠DCB,
CE=CB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAE=∠CDB.
∵∠CAE+∠AGC=90°,∠AGC=∠DGM,
∴∠CDB+∠DGM=90°,
∴∠AMD=90°,
∴AE⊥BD.

5. 如图①,在$\triangle ABC和\triangle ADE$中,$AB = AC$,$AD = AE$,$\angle BAC = \angle DAE$,连接$BD$,$CE$,$BD和CE相交于点F$,若$\triangle ABC$不动,将$\triangle ADE绕点A$任意旋转一个角度。
(1) 求证:$\triangle BAD\cong\triangle CAE$;
(2) 如图①,若$\angle BAC = \angle DAE = 90^{\circ}$,判断线段$BD与CE$的关系,并说明理由;
(3) 如图②,若$\angle BAC = \angle DAE = 60^{\circ}$,求$\angle BFC$的度数;
(4) 如图③,若$\angle BAC = \angle DAE = \alpha$,直接写出$\angle BFC$的度数(不需要说明理由)。

答案:5.
(1)证明:
∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE.
在△BAD和△CAE中,{AB=AC,
∠BAD=∠CAE,
AD=AE,
∴△BAD≌△CAE(SAS).
(2)解:BD⊥CE且BD=CE.理由如下:
由
(1)知△BAD≌△CAE,
∴∠ABD=∠ACE,BD=CE.
∵∠BAC=90°,
∴∠CBF+∠BCF=∠ABC+∠ACB=90°,
∴∠BFC=90°,
∴BD⊥CE.
(3)解:由
(2)得∠CBF+∠BCF=∠ABC+∠ACB,
∴∠BFC=∠BAC.
∵∠BAC=60°,
∴∠BFC=60°.
(4)解:∠BFC=α.