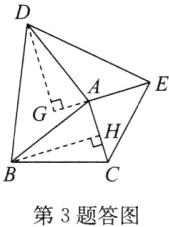
1. 如图,以$\triangle ABC的边AB$,$AC$为边,向外作等边三角形$ABD和等边三角形ACE$,连接$BE$,$CD$,相交于点$F$。
(1) 求证:$\triangle DAC\cong\triangle BAE$;
(2) 求证:$BE = DC$;
(3) 求$\angle DFE$的度数。
答案:1.
(1)证明:
∵△ABD和△ACE都为等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE.
在△DAC和△BAE中,{AD=AB,
∠DAC=∠BAE,
AC=AE,
∴△DAC≌△BAE(SAS).
(2)证明:由
(1)知△DAC≌△BAE,
∴BE=DC.
(3)解:由
(1)知△DAC≌△BAE,
∴∠ACD=∠AEB,
则∠DFE=∠FEC+∠FCE=∠FEC+∠ACD+∠ACE=∠FEC+∠AEB+∠ACE=∠AEC+∠ACE=120°.
2. (1) 如图①,已知$\triangle ABC$为等边三角形,$D为边BC$上一动点(不与点$B$,$C$重合),以$AD为边向右侧作等边三角形ADE$,连接$CE$,求证:$\triangle ABD\cong\triangle ACE$;
(2) 如图②,若点$D在边BC$的延长线上,随着动点$D$的位置不同,猜想并证明$AB与CE的位置关系及线段EC$,$AC$,$CD$之间的数量关系。

答案:2.
(1)证明:
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC−∠DAC=∠DAE−∠DAC,即∠BAD=∠CAE.
在△ABD和△ACE中,{AB=AC,
∠BAD=∠CAE,
AD=AE,
∴△ABD≌△ACE(SAS).
(2)解:AB//CE,EC=AC+CD.证明如下:
由
(1)得△ABD≌△ACE,
∴∠B=∠ACE=60°,CE=BD.
∵∠B=∠BAC,
∴∠BAC=∠ACE,
∴AB//CE.
∵CE=BD,AC=BC,
∴CE=BD=BC+CD=AC+CD.
3. 如图,分别以$\triangle ABC的边AB$,$AC为边向外作等腰直角三角形ABD和等腰直角三角形ACE$,$\angle BAD = 90^{\circ}$,$\angle CAE = 90^{\circ}$。
(1) 如图①,连接$BE$,$CD$,求证:$BE = CD$;
(2) 如图②,连接$DE$,求证:$S_{\triangle ABC} = S_{\triangle ADE}$。

答案:3.证明:
(1)
∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.
在△CAD和△EAB中,{AC=AE,
∠CAD=∠EAB,
AD=AB,
∴△CAD≌△EAB(SAS),
∴BE=CD.
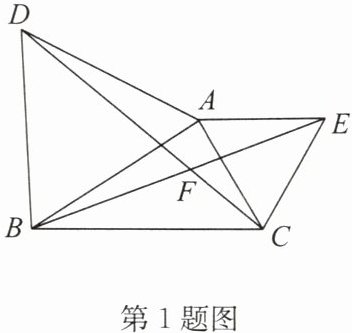
(2)如答图,作DG⊥EA交EA的延长线于点G,BH⊥AC于点H,则∠AGD=∠AHB=90°.
∵∠CAE=90°,
∴∠CAG=90°=∠BAD,
∴∠DAG=∠BAH.
在△ADG和△ABH中,{∠AGD=∠AHB,
∠DAG=∠BAH,
AD=AB,
∴△ADG≌△ABH(AAS),
∴DG=BH.
∵S△ABC=$\frac{1}{2}$AC·BH,S△ADE=$\frac{1}{2}$AE·DG,
∴S△ABC=S△ADE.