2025年启东中学作业本八年级数学上册人教版第71页解析答案

8. 如图,$\triangle ABC$为等边三角形,$AE = CD$,$AD$,$BE相交于点P$。
(1)求证：$\triangle ABE \cong \triangle CAD$；
(2)求$\angle BPD$的度数；
(3)若$BQ \perp AD于点Q$,$PQ = 6$,$PE = 2$,求$AD$的长。

答案：
(1)证明:
∵△ABC是等边三角形，
∴∠BAC=∠C=60°,AB=CA.
　在△ABE和△CAD中,AB=CA,
　∠BAE=∠C,
　AE=CD,
∴△ABE≌△CAD(SAS).
(2)解:
∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠ABE+∠BAP=∠CAD+∠BAP,
　即∠BPD=∠BAC=60°.
(3)解:
∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=30°,
∴BP=2PQ=12,
∴BE=BP+PE=12+2=14.
∵△ABE≌△CAD,
∴AD=BE=14.

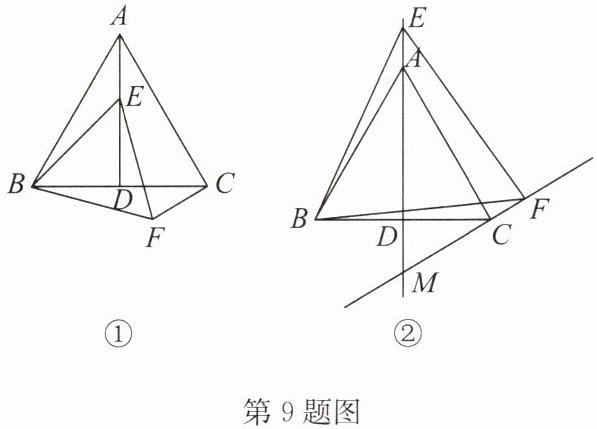
9. 已知$\triangle ABC$为等边三角形,$AD为\triangle ABC$的角平分线,动点$E在直线AD$上(不与点$A$重合),连接$BE$。以$BE为一边在BE的下方作等边三角形BEF$,连接$CF$。
(1)如图①,若点$E在线段AD$上,且$DE = BD$,则$\angle CBF$的度数是______

15°

。
(2)如图②,若点$E在AD$的反向延长线上,且直线$AE$,$CF交于点M$。
①求$\angle AMC$的度数；
②若$\triangle ABC的边长为8$,$P$,$Q为直线CF$上的两个动点,且$PQ = 10$,连接$BP$,$BQ$。$\triangle BPQ$的面积是否为定值？若是,请求出这个定值；若不是,请说明理由。

(2)解:①
∵△ABC,△BEF都是等边三角形,
∴∠ABC=∠EBF=60°,BA=BC,BE=BF,
∴∠ABE=∠CBF,
∴△ABE≌△CBF(SAS),
∴∠BAE=∠BCF;
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
∴∠BAE=∠BCF=150°,
∴∠DCM=180°−150°=30°.
∵∠CDM=90°,
∴∠AMC=90°−30°=60°.
　②△BPQ的面积是定值，定值为20.求解如下:
　过点B作BH⊥CM于点H,如答图.
　在Rt△CBH中,CB=8,∠BCH=30°,
∴BH=$\frac{1}{2}$BC=4,
∴△BPQ的面积=$\frac{1}{2}$PQ·BH=$\frac{1}{2}$×10×4=20.

答案：
(1)15°
(2)解:①
∵△ABC,△BEF都是等边三角形,
∴∠ABC=∠EBF=60°,BA=BC,BE=BF,
∴∠ABE=∠CBF,
∴△ABE≌△CBF(SAS),
∴∠BAE=∠BCF;
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
∴∠BAE=∠BCF=150°,
∴∠DCM=180°−150°=30°.
∵∠CDM=90°,
∴∠AMC=90°−30°=60°.
　②△BPQ的面积是定值，定值为20.求解如下:
　过点B作BH⊥CM于点H,如答图.
　在Rt△CBH中,CB=8,∠BCH=30°,
∴BH=$\frac{1}{2}$BC=4,
∴△BPQ的面积=$\frac{1}{2}$PQ·BH=$\frac{1}{2}$×10×4=20.