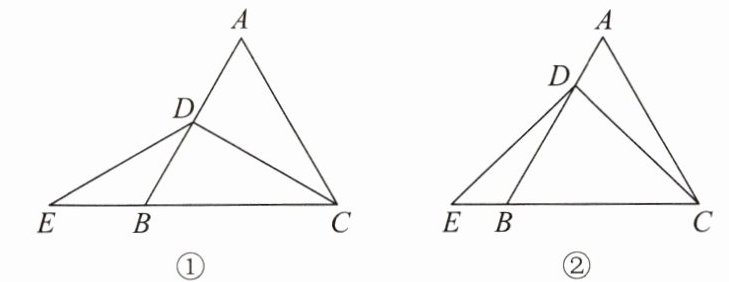
7. 已知$\triangle ABC$是等边三角形,$D是边AB$上一点,$E是CB$延长线上一点,$DC = DE$。
(1)如图①,若$D是AB$的中点,求证:$BE = AD$;
(2)如图②,若$D是AB$上任意一点(不与点$A$,$B$重合),$BE = AD$还成立吗?请说明理由。
答案:(1)证明:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AC=BC;
∵D是AB的中点,
∴∠CDB=90°,∠DCB=$\frac{1}{2}$∠ACB=30°.
∵DC=DE,
∴∠E=∠DCB=30°.
∵∠EDB=∠ABC−∠E=30°,
∴∠EDB=∠E=30°,
∴BE=BD.
∵BD=AD,
∴BE=AD.
(2)解:BE=AD还成立.理由如下:
过点D作DF//CB,交AC于点F,如答图.
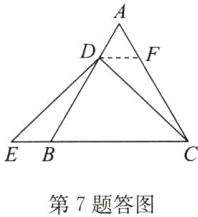
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,
∴∠ABE=180°−∠ABC=120°,
∵DF//BC,
∴∠ADF=∠ABC=60°,∠AFD=∠ACB=60°,
∴∠CFD=180°−∠AFD=120°,
∴∠ABE=∠CFD=120°.
∵∠A=∠ADF=∠AFD=60°,
∴△ADF是等边三角形,
∴AD=DF.
∵DE=DC,
∴∠E=∠DCE;
∵DF//BC,
∴∠DCB=∠FDC,
∴∠E=∠FDC,
∴△DBE≌△CFD(AAS),
∴BE=DF,
∴BE=AD.
8. (2024 春·上海期末)如图,$B是线段AE$上一点,$AB = 3BE$,$\triangle ABC与\triangle BDE$都是等边三角形,连接$AD$,$CE交于点P$,过点$B作BG\perp AD$,$BH\perp CE$,垂足分别为$G$,$H$,连接$GH$。如果$\triangle ABC的面积是S$,$AD的长是a$,求$GH$的长。(用含字母$S和a$的代数式表示)


答案:解:
∵△ABC和△BDE都是等边三角形,
∴AB=CB,∠ABC=60°,BD=BE,∠DBE=60°,
∴∠CBD=180°−∠ABC−∠DBE=60°,
∴∠ABD=∠ABC+∠CBD=120°,∠CBE=∠CBD+∠DBE=120°,即∠ABD=∠CBE;
在△ABD和△CBE中,{AB=CB,∠ABD=∠CBE,BD=BE}
∴△ABD≌△CBE(SAS),
∴∠BAD=∠BCE,AD=CE=a.
∵BG⊥AD,BH⊥CE,
∴∠AGB=∠CHB=90°.
在△ABG和△CBH中,{∠AGB=∠CHB=90°,∠BAG=∠BCH,AB=CB}
∴△ABG≌△CBH(AAS),
∴BG=BH,∠ABG=∠CBH,
∴∠ABC+∠CBG=∠CBD+∠DBH.
∵∠ABC=∠CBD=60°,
∴∠CBG=∠DBH,
∴∠GBH=∠GBD+∠DBH=∠GBD+∠CBG=∠CBD=60°,
∴△BGH为等边三角形,
∴GH=BH=BG,
∴S△CBE=$\frac{1}{2}$CE·BH=$\frac{1}{2}$a·GH.
∵AB=3BE,△ABC的面积是S,
∴S△ABC=3S△CBE,即S=3×$\frac{1}{2}$a·GH,
∴GH=$\frac{2S}{3a}$.
9. $\triangle ABC$为等边三角形,$D为射线BC$上一点,$\angle ADE = 60^{\circ}$,$DE与\triangle ABC的外角平分线交于点E$。
(1)如图①,若点$D在边BC$上,求证:$CA = CD + CE$;
(2)如图②,若点$D在边BC$的延长线上,写出$CA$,$CD$,$CE$之间的数量关系并证明。

答案:(1)证明:如答图①,在CA上截取CM=CD,连接DM.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴△CDM是等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°,
∴∠AMD=120°.
∵∠ADE=60°,
∴∠ADE=∠MDC,
∴∠ADM=∠EDC.
∵DE与△ABCの外角平分线交于点E,
∴∠ACE=60°,
∴∠DCE=120°=∠AMD.
在△ADM和△EDC中,{∠ADM=∠EDC,MD=CD,∠AMD=∠ECD}
∴△ADM≌△EDC(ASA),
∴AM=CE,
∴CA=CM+AM=CD+CE.

(2)解:CA=CE−CD.证明如下:
如答图②,在AC的延长线上截取CM=CD,连接DM.
∵△ABCは等边三角形,
∴∠ACB=60°,
∴∠DCM=60°,
∴△CDMは等边三角形,
∴MD=CD=CM,∠CMD=∠CDM=60°.
∵DE与△ABCの外角平分线交于点E,
∴∠ACE=∠DCE=60°,
∴∠ECD=∠AMD.
∵∠ADE=60°,
∴∠ADE=∠CDM,
∴∠ADM=∠EDC;
在△ADM和△EDC中,{∠ADM=∠EDC,MD=CD,∠AMD=∠ECD}
∴△ADM≌△EDC(ASA),
∴AM=EC,
∴CA=AM−CM=CE−CD.