6. 在$\triangle ABC$中,$∠BAC= 90^{\circ },∠C= 30^{\circ }$. 用无刻度的直尺和圆规在 BC 边上找一点 D,使$\triangle ACD$为等腰三角形,在如图所示的作法中,正确的有
3
个.
答案:3
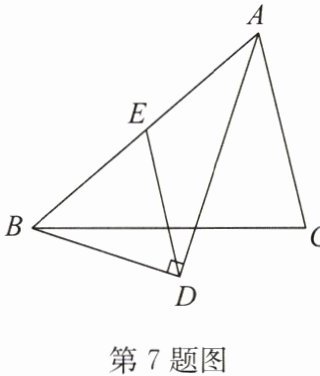
7. 如图,在$\triangle ABC$中,AD 平分$∠BAC,BD⊥AD$于点 D,过点 D 作$DE// AC$交 AB 于点 E. 求证:E 为 AB 的中点.
答案:证明:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DE//AC,
∴∠EDA=∠CAD,
∴∠EDA=∠BAD,
∴EA=ED.
∵BD⊥AD,
∴∠ADB=90°,
∴∠ADE+∠BDE=90°,∠DAB+∠ABD=90°,
∴∠ABD=∠BDE,
∴EB=ED.
∴EB=EA,即E为AB的中点
8. 已知在$\triangle ABC$中,$∠C= 3∠B$,AD 平分$∠BAC$交 BC 于点 D.
(1)如图①,若$AE⊥BC$于点E,$∠C= 75^{\circ }$,求$∠DAE$的度数;
(2)如图②,若$DF⊥AD$交 AB 于点 F,求证:$BF= DF.$

答案:
(1)解:
∵∠C=3∠B,∠C=75°,
∴∠B=25°,
∴∠BAC=180°−∠B−∠C=80°,
∵AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=40°,
∴∠ADE=∠BAD+∠B=65°.
∵AE⊥BC,
∴∠AED=90°,
∴∠DAE=90°−∠ADE=90°−65°=25°.
(2)证明:设∠B=α,则∠C=3α,
∴∠BAC=180°−∠B−∠C=180°−4α.
∵AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°−4α)=90°−2α.
∵DF⊥AD,
∴∠ADF=90°,
∴∠AFD=90°−∠BAD=90°−(90°−2α)=2α.
∵∠AFD=∠B+∠BDF,
∴∠BDF=α=∠B,
∴BF=DF;
9. 在$\triangle ABC$中,$AB= AC(AB\lt BC)$,在 BC 上截取$BD= AB$,连接 AD. 在$\triangle ABC的外部作∠ABE= ∠DAC$,且 BE 交 DA 的延长线于点 E.
(1)如图①,当$∠ABC= $______°时,$AE= AC.$
(2)如图②.
①求证:$BE= DE;$
②延长 AD 到点 F,使$DF= AE$,连接 BF,CF. 补全图形,猜想$∠BFE与∠AFC$的数量关系,并加以证明.

答案:(1)36
(2)①证明:
∵AB=AC,
∴∠ABC=∠C;
∵∠DBE=∠CBA+∠ABE,∠BDE=∠DAC+∠C,∠ABE=∠DAC,
∴∠DBE=∠BDE,
∴BE=DE;
②解:补全的图形如答图所示,∠BFE=∠AFC.

证明如下:过点B作BG⊥EF于点G,如答图,
∵DF=AE,
∴AE+AD=DF+AD,即DE=AF;
∵BE=DE,
∴BE=AF.
在△ABE和△CAF中,$\left\{\begin{array}{l} BE=AF,\\ ∠ABE=∠CAF,\\ AB=CA,\end{array}\right.$
∴△ABE≌△CAF(SAS),
∴∠E=∠AFC;
∵BA=BD,BG⊥EF,
∴DG=AG;
∵DF=AE,
∴DG+DF=AG+AE,即FG=EG;
∵BG⊥EF于点G,
∴BE=BF,
∴∠BFE=∠E,
∴∠BFE=∠AFC;