1. 生物小组的同学想用 18 m 长的篱笆围成一个等腰三角形区域作为苗圃. 如果苗圃的一边长是4m,那么苗圃的另外两边长分别是 (
C
)
A.4 m,4 m
B.4 m,10 m
C.7 m,7 m
D.7 m,7 m 或 4 m,10 m
答案:C
解析:
情况1:若4m为腰长,则底边长为18-4-4=10m。因为4+4=8<10,不满足三角形两边之和大于第三边,舍去。
情况2:若4m为底边长,则腰长为(18-4)÷2=7m。因为7+7=14>4,7+4=11>7,满足三角形三边关系。
C
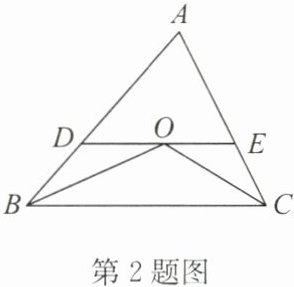
2. 如图,在$\triangle ABC$中,$AB= BC,BO,CO分别平分∠ABC和∠ACB$,过点O作$DE// BC$,分别交边 AB,AC 于点 D,E. 如果$\triangle ABC$的周长为 14,$\triangle ADE$的周长为 9,那么 AC 的长为______
4
.
答案:4
解析:
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∵DE//BC,
∴∠DOB=∠CBO,
∴∠ABO=∠DOB,
∴BD=OD,
同理可得CE=OE,
∵△ADE的周长为9,
∴AD+DE+AE=AD+DO+OE+AE=AD+BD+CE+AE=AB+AC=9,
∵△ABC的周长为14,
∴AB+BC+AC=14,
∵AB=BC,
∴AB+AB+AC=14,
即2AB+AC=14,
又
∵AB+AC=9,
∴AB=14-9=5,
∴AC=9-AB=9-5=4.
4
3. 如图,在$\triangle ABC$中,$BC= 8,∠B= 2∠C$,D 为边 AC 的垂直平分线与边 BC 的交点,且$BD= AB-2.$
(1)求证:$AB= AD;$
(2)求 CD 的长.

答案:
(1)证明:
∵D为边AC的垂直平分线与边BC的交点,
∴DC=AD,
∴∠C=∠CAD,
∴∠ADB=∠C+∠CAD=2∠C=∠B,
∴AB=AD.
(2)解:
∵AB=AD,CD=AD,BD=AB−2,BC=8,
∴CD+CD−2=8,
∴CD=5.
4. 如图,已知$\triangle ABC$,给出下列四组条件:①在$\triangle ABC$中,$AB= AC$;②在$\triangle ABC$中,$∠B= 56^{\circ },$$∠BAC= 68^{\circ }$;③在$\triangle ABC$中,$AD⊥BC$,AD 平分$∠BAC$;④在$\triangle ABC$中,$AD⊥BC$,AD 平分边 BC. 其中能判定$\triangle ABC$是等腰三角形的共有 (
D
)
A.1组
B.2组
C.3组
D.4组
答案:D
解析:
①在$\triangle ABC$中,$AB=AC$,根据等腰三角形定义,$\triangle ABC$是等腰三角形;
②在$\triangle ABC$中,$\angle B=56^{\circ}$,$\angle BAC=68^{\circ}$,则$\angle C=180^{\circ}-\angle B-\angle BAC=180^{\circ}-56^{\circ}-68^{\circ}=56^{\circ}$,$\angle B=\angle C$,所以$AB=AC$,$\triangle ABC$是等腰三角形;
③在$\triangle ABC$中,$AD\perp BC$,$AD$平分$\angle BAC$,则$\angle BAD=\angle CAD$,$\angle ADB=\angle ADC=90^{\circ}$,$AD=AD$,$\triangle ABD\cong\triangle ACD(ASA)$,$AB=AC$,$\triangle ABC$是等腰三角形;
④在$\triangle ABC$中,$AD\perp BC$,$AD$平分边$BC$,则$BD=CD$,$\angle ADB=\angle ADC=90^{\circ}$,$AD=AD$,$\triangle ABD\cong\triangle ACD(SAS)$,$AB=AC$,$\triangle ABC$是等腰三角形;
能判定$\triangle ABC$是等腰三角形的共有4组。
D
5. (2024 春·青山区期末)如图,在$3×3$的网格中,以 AB 为一边,点 P 在格点处,使$\triangle ABP$为等腰三角形的点 P 有 (
A
)
A.5个
B.3个
C.2个
D.1个
答案:A
解析:
以AB为腰:
以A为圆心,AB长为半径画圆,与格点交于3个点;
以B为圆心,AB长为半径画圆,与格点交于2个点。
以AB为底边:
作AB的垂直平分线,与格点交于0个点。
共3+2+0=5个点。
A