9. 如图,在△ABC 中,AB= AC,BD⊥AC 于点 D,求证:∠A= 2∠CBD.
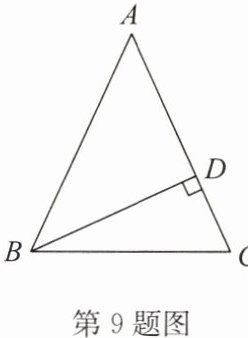
答案:证明:过点A作AE⊥BC于点E,如答图.
∵AB = AC,
∴∠BAC = 2∠CAE;
∵BD⊥AC,
∴∠BDC = ∠AEC = 90°,
∴∠CBD = 90° - ∠C,∠CAE = 90° - ∠C,
∴∠CBD = ∠CAE,
∴∠BAC = 2∠CBD.
10. 如图,在△ABC 中,AB= AC,点 D 在边 BC 上,且 AD= AE.
(1)若∠BAC= 90°,∠BAD= 30°,求∠EDC 的度数;
(2)若∠BAC= α(α>30°),∠BAD= 30°,求∠EDC 的度数;
(3)直接写出∠EDC 与∠BAD 之间的数量关系.

答案:解:
(1)
∵∠BAC = 90°,AB = AC,
∴∠B = ∠C = $\frac{1}{2}$(180° - ∠BAC) = 45°,
∴∠ADC = ∠B + ∠BAD = 45° + 30° = 75°.
∵∠DAC = ∠BAC - ∠BAD = 90° - 30° = 60°,AD = AE,
∴∠ADE = ∠AED = $\frac{1}{2}$(180° - ∠DAC) = 60°,
∴∠EDC = ∠ADC - ∠ADE = 75° - 60° = 15°.
(2)同
(1)得∠B = ∠C = $\frac{1}{2}$(180° - ∠BAC) = 90° - $\frac{1}{2}$α,
∴∠ADC = ∠B + ∠BAD = 90° - $\frac{1}{2}$α + 30° = 120° - $\frac{1}{2}$α.
∵∠DAC = ∠BAC - ∠BAD = α - 30°,AD = AE,
∴∠ADE = ∠AED = $\frac{1}{2}$(180° - ∠DAC) = 105° - $\frac{1}{2}$α,
∴∠EDC = ∠ADC - ∠ADE = (120° - $\frac{1}{2}$α) - (105° - $\frac{1}{2}$α) = 15°.
(3)∠EDC = $\frac{1}{2}$∠BAD.
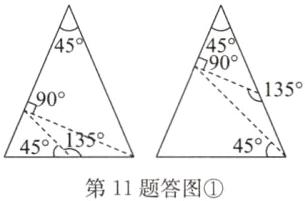
11. 如图①,用两条线段(虚线)将一个顶角为 36°的等腰三角形分成了三个小等腰三角形,并标出了三个小等腰三角形顶角的度数.
(1)请你仿照图①的方法,在图②中,用两种不同的分割方法将顶角为 45°的等腰三角形分成三个小等腰三角形.
(2)在△ABC 中,∠B= 30°,请用线段 AD 和 DE(点 D 在 BC 边上,点 E 在 AC 边上)将△ABC 分成三个小等腰三角形,且 AD= BD,DE= CE.
①试仿照图①,在图③中画出示意图;
②求∠C 的所有可能度数.

答案:解:
(1)如答图①.
(2)①如答图②所示.

②当AD = AE时,2x + x = 30° + 30°,解得x = 20°;当AD = DE时,30° + 30° + 2x + x = 180°,解得x = 40°.综上可知,∠C的度数是20°或40°.