1. 下列说法错误的是 (
D
)
A.等腰三角形两腰上的高相等
B.等腰三角形两腰上的中线相等
C.等腰三角形两底角的平分线相等
D.等腰三角形中的高、中线和角平分线重合
答案:D
2. (2024·石家庄一模)对于题目:“在△ABC 中,AB= AC,∠ABC= 70°,分别以点 A,B 为圆心,AB 长为半径的两条弧相交于点 P,求∠APC 的度数”,嘉嘉求解的结果是∠APC= 80°. 淇淇说:“嘉嘉的解答正确但不全面,∠APC 还有另一个不同的值.”则下列判断中,正确的是(
A
)
A.淇淇说得对,∠APC 的另一个值是 40°
B.淇淇说得不对,∠APC 只能等于 80°
C.嘉嘉求的结果不对,∠APC 应等于 85°
D.两人都不对,∠APC 应有 3 个不同的值
答案:A
解析:
∵AB=AC,∠ABC=70°,
∴∠ACB=∠ABC=70°,∠BAC=180°-70°×2=40°。
以A、B为圆心,AB长为半径画弧交于点P,分两种情况:
情况1:点P在AB下方
∵AP=AB,BP=AB,
∴AP=BP=AB,△ABP为等边三角形,∠BAP=60°。
∵AC=AB=AP,
∴△APC为等腰三角形,∠CAP=∠BAP-∠BAC=60°-40°=20°。
∠APC=(180°-∠CAP)/2=(180°-20°)/2=80°。
情况2:点P在AB上方
同理△ABP为等边三角形,∠BAP=60°,∠CAP=∠BAC+∠BAP=40°+60°=100°。
△APC为等腰三角形,∠APC=(180°-∠CAP)/2=(180°-100°)/2=40°。
综上,∠APC=80°或40°,淇淇说得对,另一个值是40°。
A
3. 等腰三角形一腰上的高与另一腰的夹角为 30°,则底角的度数为
$60^{\circ}$或$30^{\circ}$
.
答案:$60^{\circ}$或$30^{\circ}$
4. 如图,在△ABC 中,AB= AC,点 D,E 分别在边 BC,AB 上,AD= DE. 如果∠CAD= 60°,∠BDE= 15°,那么∠C 的度数是
$35^{\circ}$
.
答案:$35^{\circ}$
解析:
设∠C = x
∵AB = AC
∴∠B = ∠C = x,∠BAC = 180° - 2x
∵∠CAD = 60°
∴∠BAD = ∠BAC - ∠CAD = 180° - 2x - 60° = 120° - 2x
∵AD = DE
∴∠AED = ∠BAD = 120° - 2x
∠BED = 180° - ∠AED = 180° - (120° - 2x) = 60° + 2x
在△BDE中,∠B + ∠BDE + ∠BED = 180°
即x + 15° + (60° + 2x) = 180°
3x + 75° = 180°
3x = 105°
x = 35°
∠C = 35°
5. 如图,在△ABC 中,AB= AC,AD 为△ABC 的角平分线. 以点 A 为圆心,AD 长为半径画弧,与 AB,AC 分别交于点 E,F,连接 DE,DF.
(1)求证:△ADE≌△ADF;
(2)若∠BAC= 80°,求∠BDE 的度数.
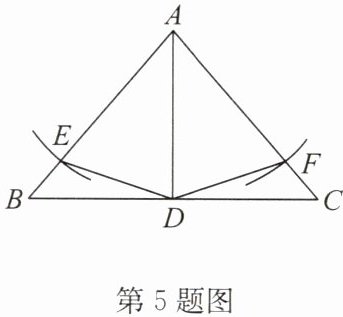
答案:
(1)证明:
∵AD是△ABC的角平分线,
∴∠BAD = ∠CAD.由作图知:AE = AF.在△ADE和△ADF中,$\begin{cases}AE = AF\\\angle EAD = \angle FAD\\AD = AD\end{cases}$
∴△ADE≌△ADF(SAS).
(2)解:
∵∠BAC = 80°,AD为△ABC的角平分线,
∴∠EAD = $\frac{1}{2}$∠BAC = 40°.由作图知:AE = AD,
∴∠AED = ∠ADE,
∴∠ADE = $\frac{1}{2}$×(180° - 40°) = 70°.
∵AB = AC,AD为△ABC的角平分线,
∴AD⊥BC.
∴∠BDE = 90° - ∠ADE = 20°.
6. 如图,在△ABC 中,AB= AC,∠BAC= 50°,∠BAC 的平分线与 AB 的垂直平分线交于点 O. 若沿 EF 折叠后点 C 与点 O 重合,则∠CEF 的度数是 (
C
)
A.60°
B.55°
C.50°
D.45°
答案:C
解析:
连接BO,CO。
∵AB=AC,∠BAC=50°,AO平分∠BAC,
∴∠BAO=∠CAO=25°,∠ABC=∠ACB=(180°-50°)/2=65°。
∵DO垂直平分AB,
∴OA=OB,∠OBA=∠BAO=25°,∠OBC=65°-25°=40°。
∵AB=AC,∠BAO=∠CAO,AO=AO,
∴△ABO≌△ACO(SAS),OB=OC,∠OCA=∠OBC=40°,∠OCE=65°-40°=25°。
∵折叠后点C与O重合,
∴EF垂直平分OC,∠OEF=∠CEF,∠OFE=90°,∠EOC=∠OCE=25°,∠CEF=90°-25°=65°-40°=25°+30°=55°。
答案:B
7. 如图,在△ABC 中,AB= AC,点 D,E 分别在 AB,AC 边上,DB= DE= AE,BE= BC,则∠BAC 的度数为
$45^{\circ}$
.
答案:$45^{\circ}$
解析:
设∠BAC = $ x $。
∵ $ AE = DE $,
∴ ∠ADE = ∠BAC = $ x $,
∴ ∠AED = $ 180^\circ - 2x $,
∴ ∠DEB = $ 180^\circ - (180^\circ - 2x) = 2x $。
∵ $ DB = DE $,
∴ ∠DBE = ∠DEB = $ 2x $,
∴ ∠BDE = $ 180^\circ - 2 × 2x = 180^\circ - 4x $。
∵ ∠ADB = $ 180^\circ $,
∴ ∠ADE + ∠BDE = $ 180^\circ $,即 $ x + (180^\circ - 4x) = 180^\circ $,解得 $ x = 0^\circ $(舍去,不合题意)。
重新推导∠DEB:∠AED = $ 180^\circ - 2x $,∠DEB = $ 180^\circ - ∠AED = 2x $(正确)。
∠ADB为平角,∠ADE = $ x $,∠BDE = $ 180^\circ - x - ∠EDC $(错误,应为∠ADB = ∠ADE + ∠EDB = $ 180^\circ $,即∠EDB = $ 180^\circ - x $)。
∵ $ DB = DE $,
∴ ∠DBE = ∠DEB = $ y $,则∠EDB = $ 180^\circ - 2y $,
∴ $ 180^\circ - 2y = 180^\circ - x $,得 $ x = 2y $,即 $ y = \frac{x}{2} $,∠DEB = $ \frac{x}{2} $。
∠AEB = ∠AED + ∠DEB = $ (180^\circ - 2x) + \frac{x}{2} = 180^\circ - \frac{3x}{2} $。
AB = AC,∠ABC = ∠ACB = $ \frac{180^\circ - x}{2} $。
BE = BC,∠BEC = ∠BCE = ∠ACB = $ \frac{180^\circ - x}{2} $。
∠AEB + ∠BEC = $ 180^\circ $,
$ 180^\circ - \frac{3x}{2} + \frac{180^\circ - x}{2} = 180^\circ $,
$ 180^\circ - \frac{3x}{2} + 90^\circ - \frac{x}{2} = 180^\circ $,
$ 270^\circ - 2x = 180^\circ $,
$ 2x = 90^\circ $,
$ x = 45^\circ $。
∠BAC = $ 45^\circ $
$ 45^\circ $
8. 如图,在△ABC 中,AB= AC,∠ABC= 30°,D,E 分别为 BC,AB 边上的动点,且∠ADE= 45°. 若△ADE 为等腰三角形,则∠DAC 的大小为
30°
.
答案:1. 首先,因为$AB = AC$,$\angle ABC=30^{\circ}$,根据等腰三角形性质$\angle C=\angle B = 30^{\circ}$,再由三角形内角和定理$\angle BAC=180^{\circ}-\angle B-\angle C$,可得:
$\angle BAC = 180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$。
2. 然后,因为$\triangle ADE$为等腰三角形,分三种情况讨论:
情况一:当$AD = AE$时:
则$\angle AED=\angle ADE = 45^{\circ}$,根据三角形内角和定理$\angle DAE=180^{\circ}-\angle ADE - \angle AED$,可得$\angle DAE=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$。
又因为$\angle BAC = 120^{\circ}$,所以$\angle DAC=\angle BAC-\angle DAE$,即$\angle DAC = 120^{\circ}-90^{\circ}=30^{\circ}$。
情况二:当$DA = DE$时:
则$\angle DAE=\angle AED$,根据三角形外角性质$\angle AED=\angle B+\angle BDE$,设$\angle BDE=x$,则$\angle AED=\angle DAE = 30^{\circ}+x$。
在$\triangle ADE$中,由三角形内角和定理$\angle DAE+\angle AED+\angle ADE = 180^{\circ}$,即$(30^{\circ}+x)+(30^{\circ}+x)+45^{\circ}=180^{\circ}$。
化简方程:$2x+105^{\circ}=180^{\circ}$,$2x=180^{\circ}-105^{\circ}=75^{\circ}$,解得$x = 37.5^{\circ}$。
所以$\angle DAE=30^{\circ}+37.5^{\circ}=67.5^{\circ}$,则$\angle DAC=\angle BAC-\angle DAE=120^{\circ}-67.5^{\circ}=52.5^{\circ}$(舍去,因为$D$,$E$是动点,这种情况不符合图形的实际情况)。
情况三:当$EA = ED$时:
则$\angle EAD=\angle ADE = 45^{\circ}$,所以$\angle DAC=\angle BAC-\angle DAE$,即$\angle DAC = 120^{\circ}-45^{\circ}=75^{\circ}$(舍去,因为$D$,$E$是动点,这种情况不符合图形的实际情况)。
综上,$\angle DAC$的大小为$30^{\circ}$。
解析:
在△ABC中,AB=AC,∠ABC=30°,则∠BAC=120°,∠C=30°。
情况1:AD=AE
∠ADE=∠AED=45°,∠DAE=90°,∠DAC=∠BAC-∠DAE=120°-90°=30°。
情况2:AD=DE
∠DAE=∠DEA=(180°-45°)/2=67.5°,∠DAC=∠BAC-∠DAE=120°-67.5°=52.5°。
情况3:AE=DE
∠DAE=∠ADE=45°,∠DAC=∠BAC-∠DAE=120°-45°=75°。
综上,∠DAC的大小为$30^{\circ}$或$52.5^{\circ}$或$75^{\circ}$。