7. 在$\triangle ABC$中,$AC= 5cm$,$AD是\triangle ABC$的中线,若$\triangle ABD的周长与\triangle ADC的周长相差2cm$,则$BA= $
3或7
$cm$。
答案:3或7
解析:
∵AD是△ABC的中线
∴BD=DC
△ABD的周长=AB+BD+AD
△ADC的周长=AC+DC+AD
∵△ABD的周长与△ADC的周长相差2cm
∴|AB+BD+AD - (AC+DC+AD)|=2cm
∵BD=DC
∴|AB - AC|=2cm
∵AC=5cm
∴|AB - 5|=2cm
当AB - 5=2时,AB=7cm
当5 - AB=2时,AB=3cm
BA=3或7cm
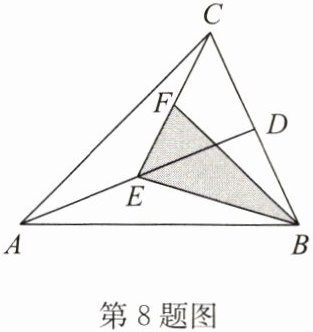
8. 如图,$D$,$E$,$F分别是BC$,$AD$,$CE$的中点,$\triangle ABC的面积是16cm^{2}$,则$\triangle BEF$的面积是
4
$cm^{2}$。
答案:4
解析:
∵D是BC中点,$\triangle ABC$面积为$16cm^2$,
$\therefore S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=8cm^2$。
∵E是AD中点,
$\therefore S_{\triangle ABE}=\frac{1}{2}S_{\triangle ABD}=4cm^2$,$S_{\triangle CBE}=\frac{1}{2}S_{\triangle ACD}=4cm^2$。
∵F是CE中点,
$\therefore S_{\triangle BEF}=\frac{1}{2}S_{\triangle CBE}=2cm^2$。
2
9. 在锐角$\triangle ABC$中,$AB= 12$,$AC= 10$,$BE$,$CD分别是\triangle ABC的边AC$,$AB$上的高,且$BE= 6$,则$CD$的长是______
5
。
答案:5
解析:
$\because BE$是$\triangle ABC$的边$AC$上的高,
$\therefore S_{\triangle ABC}=\frac{1}{2}× AC× BE$。
$\because AC=10$,$BE=6$,
$\therefore S_{\triangle ABC}=\frac{1}{2}×10×6=30$。
$\because CD$是$\triangle ABC$的边$AB$上的高,$AB=12$,
$\therefore S_{\triangle ABC}=\frac{1}{2}× AB× CD$,即$30=\frac{1}{2}×12× CD$。
解得$CD=5$。
5
10. (2024•泰州姜堰期中)如图,$G是\triangle ABC$的重心。
(1)$\frac{AD}{AB}= $
$\frac{1}{2}$
;(2)若$DG= 2$,则$CD$的长是
6
。

答案:
(1)$\frac{1}{2}$
(2)6
11. (2024•徐州期中)如图,$D是∠ABC$的平分线上的一点,过点$D作EF// BC$,$DG// AB$。
(1)若$AD⊥BD$,$∠BED= 130^{\circ}$,求$∠BAD$的度数;
(2)连接$EG$,交$BD于点O$,$DO是\triangle DEG$的角平分线吗?请说明理由。

答案:解:
(1)
∵EF//BC,∠BED=130°,
∴∠EBC=50°,又
∵BD平分∠EBC,
∴∠EBD=∠DBC=25°,又
∵AD⊥BD,
∴∠BDA=90°,
∴∠BAD=90°-25°=65°.
(2)DO是△DEG的角平分线.理由:
∵EF//BC,DG//AB,
∴∠EDB=∠DBG,∠EBD=∠GDB.
∵BD平分∠ABC,
∴∠EBD=∠GBD,
∴∠GDB=∠EDB,
∴DB平分∠EDG,
∴DO是△DEG的角平分线.
12. 如图,$\triangle ABC$中,$∠C= 90^{\circ}$,$AC= 8cm$,$BC= 6cm$,$AB= 10cm$。若动点$P从点C$开始,按$C→A→B→C$的路径运动,且速度为每秒$2cm$。设运动的时间为$t\ s$。
(1)当$t$为何值时,$CP把\triangle ABC$的周长分成相等的两部分?
(2)当$t$为何值时,$CP把\triangle ABC$的面积分成相等的两部分?
(3)当$t$为何值时,$\triangle BCP的面积为12cm^{2}$?

答案:解:
(1)
∵AC=8cm,BC=6cm,AB=10cm,
∴△ABC的周长=8+6+10=24(cm),
∴当CP把△ABC的周长分成相等的两部分时,点P在AB边上,此时CA+AP=BP+BC=12cm,
∴2t=12,t=6.
(2)当点P在AB的中点处时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),
∴2t=13,t=6.5.
(3)分两种情况:①当点P在AC边上时,
∵△BCP的面积=12cm²,
∴$\frac{1}{2}$×6×CP=12(cm²),
∴CP=4cm,
∴2t=4,t=2.②当点P在AB边上时,
∵△BCP的面积=12cm²=△ABC面积的一半,
∴P为AB的中点,
∴2t=13,t=6.5.故t为2或6.5时,△BCP的面积为12cm².