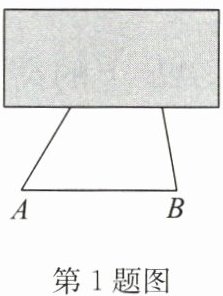
1. 如图是一个建筑工地的三角形ABC支撑架,它的上部∠ACB被一个长方形钢架遮挡,测量得∠A= 60°,∠B= 80°,则被遮挡的∠ACB的度数为 (
B
)
A.30°
B.40°
C.50°
D.60°
答案:B
解析:
在△ABC中,∠A+∠B+∠ACB=180°
∠ACB=180°-∠A-∠B=180°-60°-80°=40°
B
2. (2023秋·成都期末)如图,在△ABC中,AD平分∠BAC交边BC于点D,DE//AB交边AC于点E.若∠B= 48°,∠C= 26°,则∠ADE的大小为 (
C
)

A.42°
B.52°
C.53°
D.54°
答案:C
解析:
在△ABC中,∠B=48°,∠C=26°,
∠BAC=180°-∠B-∠C=180°-48°-26°=106°.
AD平分∠BAC,
∠BAD=$\frac {1}{2}∠BAC=$=53°.
DE//AB,
∠ADE=∠BAD=53°.
C
3. 在下列条件:①∠A+∠B= ∠C,②∠A:∠B:∠C= 5:3:2,③∠A= 90°-∠B,④∠A= 2∠B= 3∠C中,能确定△ABC是直角三角形的有 (
C
)
A.1个
B.2个
C.3个
D.4个
答案:1. 首先看条件①:
因为三角形内角和$\angle A+\angle B+\angle C = 180^{\circ}$,又$\angle A+\angle B=\angle C$。
把$\angle A+\angle B=\angle C$代入$\angle A+\angle B+\angle C = 180^{\circ}$,得$\angle C+\angle C = 180^{\circ}$,即$2\angle C = 180^{\circ}$,解得$\angle C = 90^{\circ}$,所以$\triangle ABC$是直角三角形。
2. 接着看条件②:
已知$\angle A:\angle B:\angle C = 5:3:2$,设$\angle A = 5x$,$\angle B = 3x$,$\angle C = 2x$。
因为$\angle A+\angle B+\angle C = 180^{\circ}$,所以$5x + 3x+2x = 180^{\circ}$。
合并同类项得$10x = 180^{\circ}$,解得$x = 18^{\circ}$。
则$\angle A = 5×18^{\circ}=90^{\circ}$,所以$\triangle ABC$是直角三角形。
3. 再看条件③:
由$\angle A = 90^{\circ}-\angle B$,可得$\angle A+\angle B = 90^{\circ}$。
因为$\angle A+\angle B+\angle C = 180^{\circ}$,所以$\angle C = 180^{\circ}-(\angle A+\angle B)=90^{\circ}$,所以$\triangle ABC$是直角三角形。
4. 最后看条件④:
已知$\angle A = 2\angle B = 3\angle C$,则$\angle B=\frac{1}{2}\angle A$,$\angle C=\frac{1}{3}\angle A$。
因为$\angle A+\angle B+\angle C = 180^{\circ}$,所以$\angle A+\frac{1}{2}\angle A+\frac{1}{3}\angle A = 180^{\circ}$。
通分得到$\frac{6\angle A + 3\angle A+2\angle A}{6}=180^{\circ}$,即$\frac{11}{6}\angle A = 180^{\circ}$,解得$\angle A=\frac{1080^{\circ}}{11}\neq90^{\circ}$,所以$\triangle ABC$不是直角三角形。
综上,①②③能确定$\triangle ABC$是直角三角形,共$3$个,答案是C。
解析:
①
∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,∠C=90°,是直角三角形;
②∠A:∠B:∠C=5:3:2,设∠A=5x,∠B=3x,∠C=2x,5x+3x+2x=180°,x=18°,∠A=90°,是直角三角形;
③∠A=90°-∠B,∠A+∠B=90°,∠C=90°,是直角三角形;
④∠A=2∠B=3∠C,设∠A=6x,∠B=3x,∠C=2x,6x+3x+2x=180°,x=180°/11,∠A=1080°/11≠90°,不是直角三角形。
综上,①②③能确定,共3个。
C
4. 如图,在△ABC中,若DE//BC,FG//AC,∠BDE= 120°,∠DFG= 115°,则∠C=
55
°.
答案:55
解析:
∵DE//BC,∠BDE=120°,
∴∠B=180° - ∠BDE=180° - 120°=60°。
∵FG//AC,∠DFG=115°,
∴∠A=180° - ∠DFG=180° - 115°=65°。
∵∠A + ∠B + ∠C=180°,
∴∠C=180° - ∠A - ∠B=180° - 65° - 60°=55°。
55
如图,在△ABC的边BC上任取一点E,作DE//AC交AB于点D,作EF//AB交AC于点F.
∵DE//AC,AB//EF,
∴∠1=
∠C
,∠3=
∠B
.(
两直线平行,同位角相等
)
∵AB//EF,
∴∠4=
∠A
.(
两直线平行,同位角相等
)
∵DE//AC,
∴∠4=
∠2
,(
两直线平行,内错角相等
)
∴∠2=
∠A
.(
等量代换
)
∵∠1+∠2+∠3= 180°,
∴∠A+∠B+∠C=
180°
.
答案:∠C ∠B 两直线平行,同位角相等
∠A 两直线平行,同位角相等
∠2 两直线平行,内错角相等
∠A 等量代换
180°
6. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠BAE= 30°,∠CAD= 20°,则∠B的度数为
50°
.
答案:50°
解析:
∵AE平分∠BAC,∠BAE=30°,
∴∠BAC=2∠BAE=60°.
∵∠CAD=20°,
∴∠BAD=∠BAC - ∠CAD=60° - 20°=40°.
∵AD⊥BC,
∴∠ADB=90°.
在△ABD中,∠B=180° - ∠ADB - ∠BAD=180° - 90° - 40°=50°.
50°