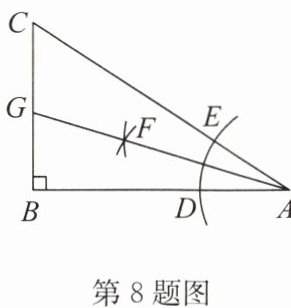
8. 如图,在$Rt△ABC$中,$∠B= 90^{\circ }$,以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E,再分别以点D,E为圆心,大于$\frac {1}{2}DE$的长为半径画弧,两弧交于点F,作射线AF交边BC于点G,若$BG= 1,AC= 4$,则$△ACG$的面积是______
2
.
答案:2
解析:
过点G作GH⊥AC于点H。
由作图步骤可知,AF是∠BAC的平分线。
因为∠B=90°,所以GB⊥AB。
又因为GH⊥AC,根据角平分线的性质,得GH=BG=1。
所以△ACG的面积为$\frac{1}{2}×AC×GH=\frac{1}{2}×4×1=2$。
2
9. 如图,在$△ABC和△CDE$中,$∠ACB= ∠DCE= 90^{\circ },AC= BC,CD= CE$.连接BD,AE,交于点F,连接CF.以下四个结论:①$BD= AE$;②$BD⊥AE$;③$∠AEC+∠DBC= 45^{\circ }$;④FC平分$∠BFE$,其中正确的是______.(填序号)

①②④
答案:①②④
10. (25分)如图,点D,E分别在AB,AC上,$∠ADC= ∠AEB= 90^{\circ }$,BE,CD相交于点O,连接AO,$OB= OC$.求证:$∠1= ∠2$.小虎同学的证明过程如下:
证明:$\because ∠ADC= ∠AEB= 90^{\circ },$
$\therefore ∠DOB+∠B= ∠EOC+∠C= 90^{\circ }.$
$\because ∠DOB= ∠EOC,$
$\therefore ∠B= ∠C$. ……第一步
又$OA= OA,OB= OC,$
$\therefore △ABO\cong △ACO$. ……第二步
$\therefore ∠1= ∠2$. ……第三步

(1)小虎同学的证明过程中,第
二
步出现错误;
(2)请写出正确的证明过程.
证明:
∵∠ADC=∠AEB=90°,
∴∠BDC=∠CEB=90°.在△DOB和△EOC中,{∠BDO=∠CEO,∠DOB=∠EOC,OB=OC,
∴△DOB≌△EOC(AAS),
∴OD=OE.在Rt△ADO和Rt△AEO中,{OA=OA,OD=OE,
∴Rt△ADO≌Rt△AEO(HL),
∴∠1=∠2.
答案:
(1)二
(2)证明:
∵∠ADC=∠AEB=90°,
∴∠BDC=∠CEB=90°.在△DOB和△EOC中,{∠BDO=∠CEO,∠DOB=∠EOC,OB=OC,
∴△DOB≌△EOC(AAS),
∴OD=OE.在Rt△ADO和Rt△AEO中,{OA=OA,OD=OE,
∴Rt△ADO≌Rt△AEO(HL),
∴∠1=∠2.
11. (25分)已知$△ABC和△ADE$均为等腰三角形,且$∠BAC= ∠DAE,AB= AC,AD= AE$.
(1)如图①,若点E在BC上,求证:$BC= BD+BE$;
(2)如图②,若点E在CB的延长线上,求证:$BC= BD-BE$.

答案:
(1)
∵∠BAC=∠DAE,
∴∠BAC-∠BAE=∠DAE-∠BAE,即∠DAB=∠EAC.又
∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴BD=CE,
∴BC=BE+CE=BD+BE.
(2)
∵∠BAC=∠DAE,
∴∠BAC+∠EAB=∠DAE+∠EAB,即∠DAB=∠EAC.又
∵AB=AC,AD=AE,
∴△DAB≌△EAC(SAS),
∴BD=CE,
∴BC=CE-BE=BD-BE.