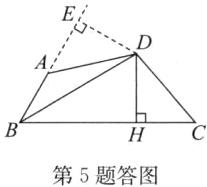
5. 如图,在四边形$ABCD$中,$BC > DA$,$AD = DC$,$BD平分\angle ABC$,$DH \perp BC于点H$.
求证:(1)$\angle DAB + \angle C = 180^{\circ}$;
(2)$BH = \frac{1}{2}(AB + BC)$.
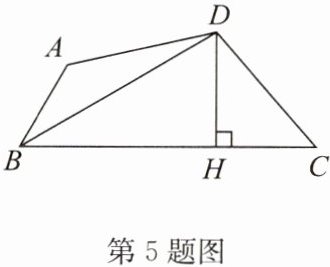
答案:(1)证明:如答图,过点D作DE⊥AB,交BA的延长线于点E.
∵BD平分∠ABC,DH⊥BC,
∴DH=DE.
在Rt△ADE和Rt△CDH中,{DA=DC,DE=DH,
∴Rt△ADE≌Rt△CDH(HL),
∴∠C=∠DAE.
∵∠DAB+∠DAE=180°,
∴∠DAB+∠C=180°.
(2)在Rt△BDE和Rt△BDH中,{BD=BD,DE=DH,
∴Rt△BDE≌Rt△BDH(HL),
∴BE=BH.
∵Rt△ADE≌Rt△CDH,
∴AE=CH,
∴AB+BC=AB+BH+CH=BE+BH=2BH,
∴BH=$\frac{1}{2}$(AB+BC).