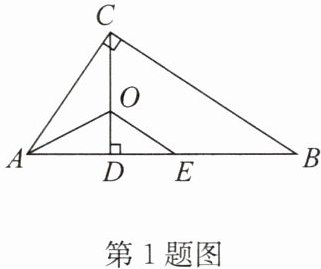
1. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD \perp AB于点D$,$AO平分\angle BAC$,交$CD于点O$,$E为AB$上一点,且$AE = AC$,求证:$OE // BC$.
类型二 利用“角平分线+垂直”构造全等三角形
答案:证明:
∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△AOC和△AOE中,{AC=AE,∠CAO=∠EAO,AO=AO,
∴△AOC≌△AOE(SAS),
∴∠ACD=∠AEO.
在△ABC中,∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=∠BCD+∠B=90°,
∴∠ACD=∠B,
∴∠AEO=∠B,
∴OE//BC.
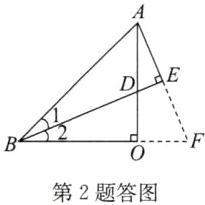
2. 如图,在$\triangle AOB$中,$OA = OB$,$\angle AOB = 90^{\circ}$,$BD平分\angle ABO交OA于点D$,$AE \perp BD$,交$BD的延长线于点E$. 求证:$BD = 2AE$.

答案:证明:如答图,延长BO,AE交于点F.
∵BD平分∠ABO,AE⊥BD,
∴∠1=∠2,∠AEB=∠FEB=90°.
在△ABE和△FBE中,{∠1=∠2,BE=BE,∠AEB=∠FEB,
∴△ABE≌△FBE,
∴AE=EF.
∵∠AOB=90°,∠AED=90°,∠ADE=∠BDO,
∴∠2=∠OAF.
∵∠AOB=90°,
∴∠DOB=∠FOA=90°.
在△OBD和△OAF中,{∠2=∠FAO,BO=AO,∠BOD=∠AOF,
∴△OBD≌△OAF,
∴BD=AF.
∵AE=EF,
∴BD=2AE.
3. 如图,在$\triangle ABC$中,$\angle ABC = 60^{\circ}$,$AD$,$CE分别平分\angle BAC$,$\angle ACB$,且两线交于点$O$.
(1)求$\angle AOC$的度数;
(2)求证:$AC = AE + CD$.

答案:(1)解:
∵∠ABC=60°,AD,CE分别平分∠BAC,∠ACB,
∴∠OAC+∠OCA=$\frac{1}{2}$(∠BAC+∠BCA)=$\frac{1}{2}$(180°−∠B)=60°,
∴∠AOC=120°.
(2)证明:如答图,在AC上截取AF=AE,连接OF;

∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△AOE和△AOF中,{AE=AF,∠EAO=∠FAO,AO=AO,
∴△AOE≌△AOF(SAS),
∴∠AOE=∠AOF.
由
(1)知∠AOC=120°,
∴∠AOE=60°,
∴∠AOF=∠COD=60°=∠COF.
∵CE平分∠ACB,
∴∠FCO=∠DCO.
在△COF和△COD中,{∠FOC=∠DOC,CO=CO,∠FCO=∠DCO,
∴△COF≌△COD(ASA),
∴CF=CD,
∴AC=AF+CF=AE+CD.
4. 如图,$P是\angle BAC的平分线AD$上一点,$AC > AB$,求证:$PC - PB < AC - AB$.

答案:证明:如答图,在AC上截取AE,使AE=AB,连接PE.

∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
在△AEP和△ABP中,{AE=AB,∠EAP=∠BAP,AP=AP,
∴△AEP≌△ABP(SAS),
∴PE=PB.
在△PCE中,PC - PE<CE,
∴PC - PE<AC - AE,
∴PC - PB<AC - AB.