7. 在$\triangle ABC$中,$AD平分\angle BAC$,交$BC于点D$,$DE\perp AB$,$DF\perp AC$,垂足分别为$E$,$F$,连接$EF$,$AD与EF交于点O$,则$AD与EF$的关系是
AD垂直平分EF
。
答案:AD垂直平分EF
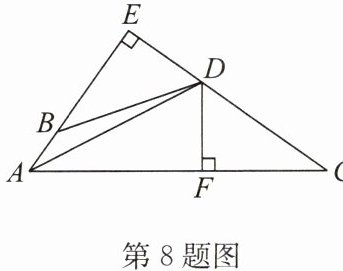
8. 如图,$DE\perp AB$,交$AB的延长线于点E$,$DF\perp AC于点F$,且$DB= DC$,$BE= CF$,求证:$AD是\angle BAC$的平分线。
答案:证明:
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.在Rt△BDE和Rt△CDF中,{∠BDE = ∠CDF,∠BED = ∠CFD}
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD是∠BAC的平分线.
9. 如图,$\triangle ABC的外角\angle ACD的平分线CP与内角\angle ABC的平分线BP交于点P$,连接$AP$。
(1)延长$BA至点E$,求证:$AP平分\angle CAE$;
(2)若$\angle BPC= 40^{\circ}$,求$\angle CAP$的度数。

(1)证明:如答图,过点P作PN⊥BD于点N,PM⊥BE 于点M,PF⊥AC于点F.
∵∠ACD的平分线CP与∠ABC的平分线BP交于点P,
∴PM=PN,PN=PF,
∴PM=PF,而PA=PA,
∴Rt△AMP≌Rt△AFP(HL),
∴∠PAE=∠PAF,
∴AP平分∠CAE.
(2)解:设∠ABC=2α,∠ACD=2β.
∵∠ACD的平分线CP与∠ABC的平分线BP交于点P,
∴β=α+∠BPC,而β=α + ∠BAC,
∴∠BAC=2∠BPC=80°,
∴∠CAP=(180° - 80°)÷2 = 50°.
答案:
(1)证明:如答图,过点P作PN⊥BD于点N,PM⊥BE 于点M,PF⊥AC于点F.
∵∠ACD的平分线CP与∠ABC的平分线BP交于点P,
∴PM=PN,PN=PF,
∴PM=PF,而PA=PA,
∴Rt△AMP≌Rt△AFP(HL),
∴∠PAE=∠PAF,
∴AP平分∠CAE.
(2)解:设∠ABC=2α,∠ACD=2β.
∵∠ACD的平分线CP与∠ABC的平分线BP交于点P,
∴β=α+∠BPC,而β=α + ∠BAC,
∴∠BAC=2∠BPC=80°,
∴∠CAP=(180° - 80°)÷2 = 50°.
10. 如图,$AB= AC$,$AD= AE$,$\angle CAB= \angle EAD$,$F为BD和CE$的交点。
(1)求证:$BD= CE$;
(2)连接$AF$,求证:$FA平分\angle BFE$。

答案:证明:
(1)
∵∠CAB=∠EAD,
∴∠CAB+∠DAC=∠EAD+∠DAC,
∴∠DAB=∠EAC.又
∵AB=AC,AD=AE,
∴△DAB≌△EAC,
∴BD=CE;
(2)过点A作AN⊥EC于点N,过点A作AM⊥BD于点M,如答图,
∴$S_{△DAB}$ = $\frac{1}{2}$×DB×AM,$S_{△EAC}$ = $\frac{1}{2}$×EC×AN,由
(1)已证明△DAB≌△EAC,BD=CE,
∴S△DAB=S△EAC,
∴$\frac{1}{2}$×DB×AM = $\frac{1}{2}$×EC×AN,
∴AM=AN.在Rt△ANF和Rt△AMF中,{AF = AF,AN = AM}
∴Rt△ANF≌Rt△AMF(HL),
∴∠AFN=∠AFM,
∴FA平分∠BFE;