1. 已知$\triangle ABC$,两个完全一样的三角板如图方式摆放,它们的一组对应直角边分别在$AB$,$AC$上,且这组对应直角边所对的顶点重合于点$M$,点$M$一定在(
A
)
A.$\angle A$的平分线上
B.$AC$边的高上
C.$BC$边的垂直平分线上
D.$AB$边的中线上
答案:A
解析:
过点$M$作$MD \perp AB$于点$D$,$ME \perp AC$于点$E$。
因为两个三角板完全一样,且一组对应直角边分别在$AB$,$AC$上,对应直角边所对顶点重合于$M$,所以$MD = ME$。
根据角平分线的判定定理,到角两边距离相等的点在角的平分线上,故点$M$在$\angle A$的平分线上。
A
2. 如图,在$\triangle ABC$中,$O是\triangle ABC$内一点,且点$O到\triangle ABC$三边的距离相等,若$\angle A= 70^{\circ}$,则$\angle BOC$的度数为(
A
)
A.$125^{\circ}$
B.$135^{\circ}$
C.$55^{\circ}$
D.$35^{\circ}$
答案:A
解析:
∵点O到△ABC三边的距离相等,
∴O是△ABC的内心,
∴BO平分∠ABC,CO平分∠ACB,
∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=125°
A
3. 如图,$PC\perp OA于点C$,$PD\perp OB于点D$,$PC= PD$,$Q是OP$上一点,$QE\perp OA于点E$,$QF\perp OB于点F$。求证:$QE= QF$。
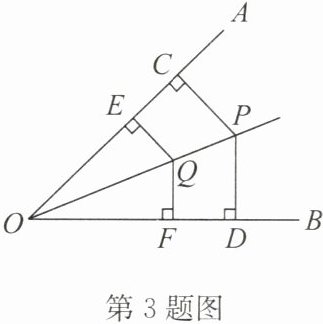
答案:证明:
∵PC⊥OA,PD⊥OB,PC=PD,
∴∠AOP=∠BOP.
∵QE⊥OA,QF⊥OB,
∴QE=QF.
4. 如图,在$\triangle ABC$中,$P$,$O分别是BC$,$AC$上的点,作$PR\perp AB$,$PS\perp AC$,垂足分别是$R$,$S$,若$AO= PO$,$PR= PS$,有三个结论:①$AS= AR$,②$OP// AR$,③$\triangle BRP\cong \triangle CSP$,其中正确的是(
C
)
A.①③
B.②③
C.①②
D.①②③
答案:C
解析:
连接AP。
∵PR⊥AB,PS⊥AC,PR=PS,
∴AP平分∠BAC,∠ARP=∠ASP=90°。
在Rt△ARP和Rt△ASP中,
$\left\{\begin{array}{l} AP=AP\\ PR=PS\end{array}\right.$
∴Rt△ARP≌Rt△ASP(HL),
∴AS=AR,①正确。
∵AO=PO,
∴∠OAP=∠OPA。
∵AP平分∠BAC,
∴∠OAP=∠RAP,
∴∠OPA=∠RAP,
∴OP//AR,②正确。
△BRP与△CSP中,仅有∠BRP=∠CSP=90°,PR=PS,无法证明全等,③错误。
综上,正确的是①②。
C
5. 如图,$\triangle ABC$中,$\angle ABC= 48^{\circ}$,$\angle ACB= 84^{\circ}$,点$D$,$E分别在BA$,$BC$的延长线上,$BP平分\angle ABC$,$CP平分\angle ACE$,连接$AP$,则$\angle PAC$的度数为______
66°
。


答案:66°
解析:
在$\triangle ABC$中,$\angle ABC=48^\circ$,$\angle ACB=84^\circ$,则$\angle BAC=180^\circ-48^\circ-84^\circ=48^\circ$。
$\angle ACE=180^\circ-\angle ACB=180^\circ-84^\circ=96^\circ$。
因为$CP$平分$\angle ACE$,所以$\angle ACP=\frac{1}{2}\angle ACE=\frac{1}{2}×96^\circ=48^\circ$。
$BP$平分$\angle ABC$,则$\angle ABP=\frac{1}{2}\angle ABC=24^\circ$。
设$\angle PAC=x$,则$\angle BAP=\angle BAC+\angle PAC=48^\circ+x$。
在$\triangle ABP$中,$\angle APB=180^\circ-\angle ABP-\angle BAP=180^\circ-24^\circ-(48^\circ+x)=108^\circ-x$。
在$\triangle APC$中,$\angle APC=180^\circ-\angle PAC-\angle ACP=180^\circ-x-48^\circ=132^\circ-x$。
因为点$D$在$BA$延长线上,所以$\angle APB+\angle APC=180^\circ$,即$(108^\circ-x)+(132^\circ-x)=180^\circ$,解得$x=30^\circ$。
$30^\circ$
6. 如图,已知$EF\perp CD$,$EF\perp AB$,$MN\perp AC$,$M是EF$的中点,只需添加
ME=MN(答案不唯一)
,就可使$CM$,$AM分别为\angle ACD和\angle CAB$的平分线。


答案:ME=MN(答案不唯一)