2025年启东中学作业本八年级数学上册人教版第37页解析答案

4. 如图,$AB\perp AC$,$AB = AC$,$D是AB$上一点,$CE\perp CD$,$CE = CD$,连接$BE交AC于点F$,求证：$F是BE$的中点.

答案：
4.证明:如答图，过点E作EH⊥AC于点H，
∴∠EHC=∠EHF=90°。
∵AB⊥AC，
∴∠DAC=90°，∠ADC+∠ACD=90°。
∵CE⊥CD，
∴∠ECH+∠ACD=90°，
∴∠ECH=∠CDA。
在△HEC和△ACD中，∠EHC=∠CAD=90°，∠ECH=∠CDA，CE=DC，
∴△HEC≌△ACD(AAS)，
∴EH=AC。
∵AB=AC，
∴EH=AB。
在△ABF和△HEF中，∠BAF=∠EHF=90°，∠AFB=∠HFE，BA=EH，
∴△ABF≌△HEF(AAS)，
∴EF=BF，
∴F是BE的中点。

5. 如图,$A$,$B$,$C$三点共线,$D$,$C$,$E$三点共线,$\angle A = \angle DBC$,$EF\perp AC于点F$,$AE = BD$.
(1)求证：$C是DE$的中点；
(2)求证：$AB = 2CF$.

答案：
5.证明:
(1)过点D作DH⊥AC，交AC的延长线于点H，如答图，
∴∠EFC=∠DHC=90°。
在△AEF和△BDH中，∠AFE=∠BHD=90°，∠A=∠DBH，AE=BD，
∴△AEF≌△BDH(AAS)，
∴EF=DH。
在△EFC和△DHC中，∠FCE=∠HCD，∠EFC=∠DHC=90°，EF=DH，
∴△EFC≌△DHC(AAS)，
∴CE=CD，
∴C是DE的中点。

(2)由
(1)得，△AEF≌△BDH，△EFC≌△DHC，
∴AF=BH，CF=CH，
∴AB+BF=BF+FH，FH=2FC，
∴AB=FH=2CF。

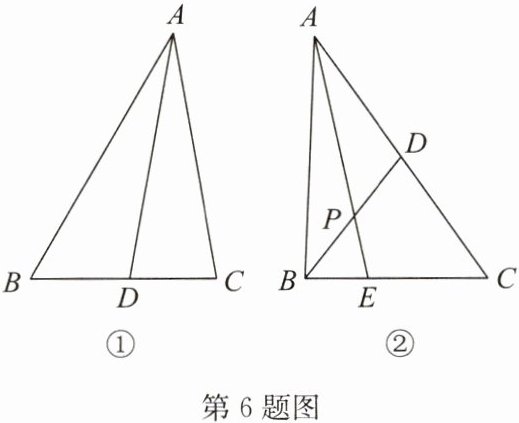
6. (1)如图①,在$\triangle ABC$中,$\angle B = 60^{\circ}$,$\angle C = 80^{\circ}$,$AD平分\angle BAC$. 求证：$AD = AC$；
(2)如图②,在$\triangle ABC$中,点$E在BC$边上,中线$BD与AE相交于点P$,$AP = BC$. 求证：$PE = BE$.

答案：
6.证明:
(1)在△ABC中，∠B=60°，∠C=80°，
∴∠BAC=180°−60°−80°=40°。
∵AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$∠BAC=20°，
∴∠ADC=∠B+∠BAD=60°+20°=80°，
∵∠C=80°，
∴∠C=∠ADC，
∴AD=AC。
(2)如答图，过点A作AF//BC交BD的延长线于点F，
∴∠F=∠DBC，∠FAD=∠C，
由题意知AD=CD，
∴△ADF≌△CDB(AAS)，
∴AF=BC，
∵AP=BC，
∴AP=AF，
∴∠APF=∠F，
∵∠APF=∠BPE，∠F=∠DBC，
∴∠BPE=∠PBE，
∴PE=BE。