2025年启东中学作业本八年级数学上册人教版第36页解析答案

1.【阅读理解】
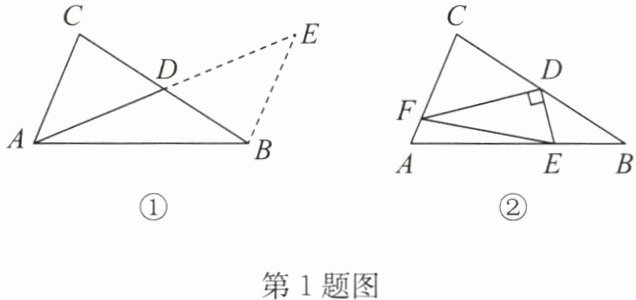
(1)如图①,在$\triangle ABC$中,若$AB = 9$,$AC = 5$,求$BC边上的中线AD$的取值范围.可以用如下方法：延长$AD至点E$,使$DE = AD$,连接$BE$.
在$\triangle ABE$中,利用三角形的三边关系可得$AD$的取值范围是____；
【问题解决】
(2)如图②,在$\triangle ABC$中,$D是BC$边的中点,$DE\perp DF于点D$,$DE交AB于点E$,$DF交AC于点F$,连接$EF$.求证：$BE + CF＞EF$.

答案：
1.
(1)2＜AD＜7
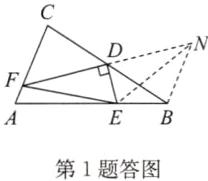
(2)证明:如答图，延长FD至点N,使DN=DF,连接BN,EN.
在△FDC和△NDB中，FD=ND，∠FDC=∠NDB，CD=BD，
∴△FDC≌△NDB(SAS)，
∴FC=BN。
∵DF=DN，DE⊥DF，
∴EF=EN。
在△EBN中，BE+BN＞EN，
∴BE+CF＞EF。

2. 如图,在$\triangle ABC和\triangle ADE$中,$AB = AC$,$AD = AE$,$\angle BAC + \angle EAD = 180^{\circ}$,连接$BE$,$CD$,$F为BE$的中点,连接$AF$. 求证：$CD = 2AF$.

答案：
2.证明:延长AF至点G,使FG=AF,连接BG,如答图。
∵F为BE的中点，
∴EF=BF。
在△AFE和△GFB中，AF=GF，∠AFE=∠GFB，EF=BF，
∴△AFE≌△GFB(SAS)。
∴∠EAF=∠G，AE=BG，
∴AE//BG，
∴∠GBA+∠BAE=180°。
∵∠BAC+∠EAD=180°，
∴∠DAC+∠BAE=180°，
∴∠GBA=∠DAC。
∵AD=AE，
∴BG=AD。
在△GBA和△DAC中，AB=CA，∠GBA=∠DAC，BG=AD，
∴△GBA≌△DAC(SAS)，
∴AG=CD。
∵AG=2AF，
∴CD=2AF。

3. 如图,$AD是\triangle ABC$的中线,点$E在BC$的延长线上,$CE = AB$,$\angle BAC = \angle BCA$,连接$AE$. 求证：$AE = 2AD$.

答案：
3.证明:如答图，延长AD至点M,使DM=AD,连接CM。
∵AD是△ABC的中线，
∴DB=CD。
在△ABD和△MCD中，BD=CD，∠ADB=∠MDC，AD=MD，
∴△ABD≌△MCD(SAS)，
∴MC=AB，∠B=∠MCD。
∵AB=CE，
∴CM=CE。
∵∠BAC=∠BCA，
∴∠B+∠BAC=∠MCD+∠BCA，即∠ACE=∠ACM。
在△ACM和△ACE中，AC=AC，∠ACM=∠ACE，CM=CE，
∴△ACM≌△ACE(SAS)，
∴AM=AE。
∵AM=2AD，
∴AE=2AD。