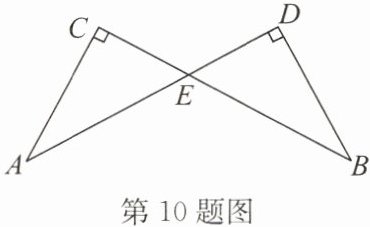
10. 如图,$∠C= ∠D= 90^{\circ },BC$与AD交于点E,$AD= BC$.求证:$AC= BD$.
答案:证明:连接AB.在Rt△ABC和Rt△BAD中,{AB=BA,BC=AD,
∴Rt△ABC≌Rt△BAD(HL),
∴AC=BD.
11. 如图,$AB= AC,DE= DF,DE⊥AB$,垂足为E,$DF⊥AC$,垂足为F.
求证:(1)$AE= AF$;(2)$DB= DC$.

答案:证明:
(1)如答图,连接AD.

∵DE⊥AB,DF⊥AC,
∴∠DEA=∠DFA=90°.在Rt△ADE和Rt△ADF中,{AD=AD,DE=DF,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF.
(2)
∵AB=AC,AE=AF,
∴BE=CF.在△BDE和△CDF中,{DE=DF,∠DEB=∠DFC,BE=CF,
∴△BDE≌△CDF(SAS),
∴DB=DC.
12. 如图,$DE⊥AB$于点E,$DF⊥AC$于点F,若$BD= CD,BE= CF$.
(1)求证:$△ADE\cong △ADF$;
(2)已知$AC= 18,AB= 12$,求BE的长.

答案:
(1)证明:
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠E=∠DFC=∠DFA=90°.在Rt△EBD与Rt△FCD中,{BD=CD,BE=CF,
∴Rt△EBD≌Rt△FCD(HL),
∴DE=DF.在Rt△AED与Rt△AFD中,{AD=AD,DE=DF,
∴Rt△AED≌Rt△AFD(HL).
(2)解:
∵Rt△AED≌Rt△AFD,
∴AE=AF,
∴AF=AB+BE=12+BE.
∵AC=AF+FC,
∴AC=AB+BE+FC,
∴18=12+BE+CF.
∵BE=CF,
∴18=12+2BE,
∴BE=3.
13. 观察与类比:
(1)如图①,在$△ABC$中,$∠ACB= 90^{\circ }$.点D在$△ABC$外,连接AD,作$DE⊥AB$于点E,延长DE交BC于点F,$AD= AB,AE= AC$,连接AF.求证:$DF= BC+CF$;
(2)如图②,$AB= AD,AC= AE,∠ACB= ∠AED= 90^{\circ }$,延长BC交DE于点F,写出DF,BC,CF之间的数量关系,并证明你的结论.

答案:(1)证明:
∵DE⊥AB,∠ACB=90°,
∴∠AED=∠AEF=∠ACB=90°.在Rt△ACF与Rt△AEF中,{AF=AF,AC=AE,
∴Rt△ACF≌Rt△AEF(HL),
∴CF=EF.在Rt△ADE与Rt△ABC中,{AD=AB,AE=AC,
∴Rt△ADE≌Rt△ABC(HL),
∴DE=BC,
∵DF=DE+EF,
∴DF=BC+CF.
(2)解:BC=CF+DF.证明如下:如答图,连接AF;

在Rt△ABC与Rt△ADE中,{AB=AD,AC=AE,
∴Rt△ABC≌Rt△ADE(HL),
∴BC=DE.
∵∠ACB=90°,
∴∠ACF=90°=∠AED.在Rt△ACF与Rt△AEF中,{AF=AF,AC=AE,
∴Rt△ACF≌△AEF(HL),
∴CF=EF.
∵DE=EF+DF,
∴BC=CF+DF;