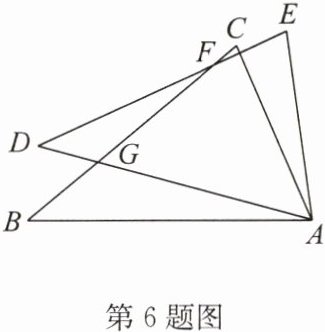
6. 如图,已知AB= AD,AC= AE,∠BAD= ∠CAE,求证:△ABC≌△ADE.
答案:证明:
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,{AB=AD,∠BAC=∠DAE,AC=AE}
∴△ABC≌△ADE(SAS).
7. (1)如图①,在Rt△ABC中,AC= BC,∠ACB= 90°,BD⊥CD于点D,AE⊥CD于点E. 求证:AE= CD;
(2)如图②,在Rt△ABC中,AC= BC,∠ACB= ∠CDB= 90°,CD= 5,求△ACD的面积.

答案:(1)证明:
∵AE⊥CD,BD⊥CD,
∴∠AEC=∠CDB=90°,
∴∠EAC+∠ACE=90°.
∵∠ACB=90°,
∴∠ACE+∠DCB=90°,
∴∠EAC=∠DCB.
在△ACE和△CBD中,{∠EAC=∠DCB,∠AEC=∠CDB=90°,AC=CB}
∴△ACE≌△CBD(AAS),
∴AE=CD.
(2)解:过点A作AE⊥CD于点E,如答图.
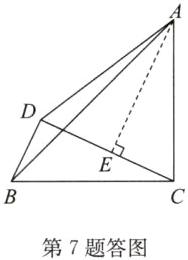
由
(1)可知:△ACE≌△CBD(AAS),
∴CD=AE=5,
∴S△ACD=$\frac{1}{2}$CD·AE=$\frac{1}{2}$×5×5=$\frac{25}{2}$.
8. 通过对“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
【模型呈现】如图①,∠BAD= 90°,AB= AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E. 求证:BC= AE;
【模型应用】如图②,AE⊥AB且AE= AB,BC⊥CD且BC= CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积为
50
;
【深入探究】如图③,∠BAD= ∠CAE= 90°,AB= AD,AC= AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G. 若BC= 21,AF= 12,则△ADG的面积为
63
.

答案:[模型呈现]证明:
∵∠BAD=90°,
∴∠BAC+∠DAE=90°.
∵BC⊥AC,DE⊥AC,
∴∠ACB=∠DEA=90°,
∴∠BAC+∠ABC=90°,
∴∠ABC=∠DAE.
在△ABC和△DAE中,{∠ABC=∠DAE,∠ACB=∠DEA,BA=AD}
∴△ABC≌△DAE(AAS),
∴BC=AE.
[模型应用]50
[深入探究]63