1. 如图,点A,D,B,E在同一条直线上,且AC// DF,AD= BE,添加一个条件,不能推导出△ABC≌△DEF的是 (
A
)
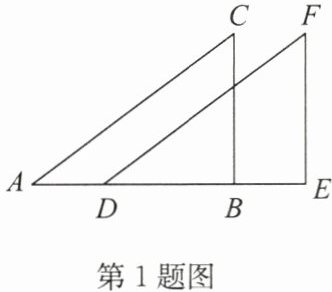
A.BC= EF
B.BC// EF
C.AC= DF
D.∠C= ∠F
答案:A
解析:
∵AC//DF,
∴∠A=∠EDF。
∵AD=BE,
∴AD+DB=BE+DB,即AB=DE。
A. BC=EF,SSA不能判定△ABC≌△DEF。
B. BC//EF,
∴∠ABC=∠E,
在△ABC和△DEF中,
$\left\{\begin{array}{l} ∠A=∠EDF\\ AB=DE\\ ∠ABC=∠E\end{array}\right.$,
∴△ABC≌△DEF(ASA)。
C. AC=DF,
在△ABC和△DEF中,
$\left\{\begin{array}{l} AC=DF\\ ∠A=∠EDF\\ AB=DE\end{array}\right.$,
∴△ABC≌△DEF(SAS)。
D. ∠C=∠F,
在△ABC和△DEF中,
$\left\{\begin{array}{l} ∠C=∠F\\ ∠A=∠EDF\\ AB=DE\end{array}\right.$,
∴△ABC≌△DEF(AAS)。
A
2. 如图,点A,D,C,F在同一条直线上,AB// DE,AC= DF,AB= DE.
(1)求证:△ABC≌△DEF;
(2)若∠A= 55°,∠E= 88°,求∠F的度数.

答案:
(1)证明:
∵AB//DE,
∴∠BAC=∠EDF.
在△ABC和△DEF中,{AC=DF,∠BAC=∠EDF,AB=DE}
∴△ABC≌△DEF(SAS).
(2)解:由
(1)可知,∠EDF=∠A=55°.
∵∠E=88°,
∴∠F=180° - ∠EDF - ∠E=37°.
3. 如图,∠DAC= ∠BAC,下列条件中,不能判定△ABC≌△ADC的是(
A
)
A.DC= BC
B.AB= AD
C.∠D= ∠B
D.∠DCA= ∠BCA
答案:A
4. 如图,AC与BD相交于点E,∠A= ∠D,EB= EC.
(1)求证:△ABC≌△DCB;
(2)若CE= CD,∠1= 40°,求∠3的度数.

答案:
(1)证明:
∵EB=EC,
∴∠1=∠2,
在△ABC和△DCB中,{∠A=∠D,∠2=∠1,BC=CB}
∴△ABC≌△DCB(AAS).
(2)解:
∵EB=EC,
∴∠1=∠2=40°,
∴∠CED=∠1 + ∠2=80°,
∵CE=CD,
∴∠D=∠CED=80°,
∴∠3=180° - 80° - 80°=20°.
5. 如图,在△ABC和△ADE中,延长BC交DE于点F,BC= DE,AC= AE,∠ACF+∠AED= 180°. 求证:AB= AD.

证明:
∵∠ACB+∠ACF=∠ACF+∠AED=180°,
∴∠ACB=∠AED.
在△ABC和△ADE中,{BC=DE,∠ACB=∠AED,AC=AE}
∴△ABC≌△ADE(SAS),
∴AB=AD.
答案:证明:
∵∠ACB+∠ACF=∠ACF+∠AED=180°,
∴∠ACB=∠AED.
在△ABC和△ADE中,{BC=DE,∠ACB=∠AED,AC=AE}
∴△ABC≌△ADE(SAS),
∴AB=AD.