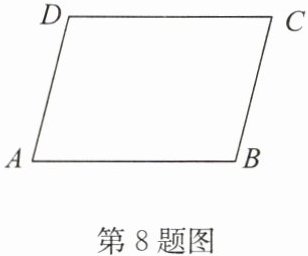
8.如图,已知$AD= CB$,$AB= CD$. 求证:$∠A= ∠C$.
答案:证明:连接 BD.在△ABD与△CDB中,$\left\{\begin{array}{l} AD=CB,\\ AB=CD,\\ BD=DB,\end{array}\right. $
∴△ABD≌△CDB(SSS),
∴∠A=∠C.
9.如图,$AB= CD$,$DE= BF$,$AE= CF$.
(1)求证:$\triangle ABE\cong \triangle CDF$;
(2)判断$AE与CF$的位置关系,并说明理由.

答案:
(1)证明:
∵DE=BF,
∴DE-EF=BF-EF,即 DF=BE.在△ABE和△CDF中,$\left\{\begin{array}{l} AB=CD,\\ BE=DF,\\ AE=CF,\end{array}\right. $
∴△ABE≌△CDF(SSS).
(2)解:AE//CF.理由:
∵△ABE≌△CDF,
∴∠AEB=∠DFC.
∵∠AEB+∠AEF=∠DFC+∠EFC=180°,
∴∠AEF=∠EFC,
∴AE//CF.
10.如图,在$\triangle ABC$中,$AC= BC$,$D是AB$上一点,$AE⊥CD于点E$,$BF⊥CD交CD的延长线于点F$,若$CE= BF$,$AE= EF+BF$,试判断直线$AC与BC$的位置关系,并说明理由.

答案:解:AC⊥BC.理由如下:
∵AE=EF+BF,CE=BF,
∴AE=EF+CE=CF.在△ACE和△CBF中,$\left\{\begin{array}{l} AC=CB,\\ AE=CF,\\ CE=BF,\end{array}\right. $
∴△ACE≌△CBF,
∴∠BCF=∠CAE.
∵AE⊥CD,
∴∠AEC=90°,
∴∠CAE+∠ACE=90°,
∴∠ACB=∠BCF+∠ACE=∠CAE+∠ACE=90°,
∴AC⊥BC.
11.小春在做数学作业时,遇到这样一个问题:如图,$AB= CD$,$BC= AD$,请说明$∠A= ∠C$. 小春动手测量了一下,发现$∠A确实等于∠C$,但她不能说明其中的道理,你能帮助她吗?

答案:解:能.连接 BD.
∵在△ABD 和△CDB 中,AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB(SSS),
∴∠A=∠C.
12.如图,$AB= AC$,$AD= AE$,$BD= CE$,$BD分别与CE$,$AC相交于点O$,$F$. 求证:$∠CAB= ∠EAD= ∠BOC$.

答案:证明:
∵AB=AC,AD=AE,BD=CE,
∴△ABD≌△ACE(SSS),
∴∠BAD=∠CAE,∠C=∠B.
∴∠BAD-∠CAD=∠CAE-∠CAD,即∠CAB=∠EAD,
∵∠BOC=180°-∠C-∠OFC=180°-∠B-∠AFB=∠CAB,
∴∠CAB=∠EAD=∠BOC.