10.已知a,b,c是△ABC的三边长,a= 4,b= 6,设三角形的周长是x.
(1)直接写出c及x的取值范围.
(2)若x是小于18的偶数,
①求c的长;
②判断△ABC的形状.
答案:10.解:
(1)因为a=4,b=6,所以2<c<10.
故三角形的周长x的取值范围为12<x<20.
(2)①因为x为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
11.用一条长24 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边长为6 cm的等腰三角形吗? 为什么?
(3)若等腰三角形的腰长为a cm,求a的取值范围.
答案:11.解:
(1)设底边长为x cm.
∵腰长是底边长的2倍,
∴腰长为2x cm,
∴2x+2x+x=24,解得x=$\frac{24}{5}$,
∴2x=2×$\frac{24}{5}$=$\frac{48}{5}$,
∴各边长分别为$\frac{48}{5}$cm,$\frac{48}{5}$cm,$\frac{24}{5}$cm.
/3
答案
(2)①当6 cm为底边长时,腰长=$\frac{24-6}{2}$=9(cm).
②当6 cm为腰长时,底边长=24-6-6=12(cm),
∵6+6=12,
∴不能构成三角形,故舍去.
∴能围成有一边长为6 cm的等腰三角形,另两边长分别为9 cm,9 cm.
(3)由题意得:$\left\{\begin{array}{l} a+a>24-2a,\\ 24-2a>0,\end{array}\right. $
解得:6<a<12.
12.已知△ABC的三边长分别是a,b,c.
(1)若a= 5,b= 6,△ABC的周长是小于18的偶数,求c的长;
(2)化简:$|a+b-c|-|c-a-b|$.
答案:12.解:
(1)
∵a,b,c是△ABC的三边长,a=5,b=6,
∴1<c<11.
∵△ABC的周长是小于18的偶数,
∴1<c<7,
∴c=3或5.
(2)|a+b-c|-|c-a-b|=a+b-c+c-a-b=0.
13.如图,在△ABC中,点D在边AB上,连接CD,点O在CD上,连接BO,求证:AB+AC>OB+OC.
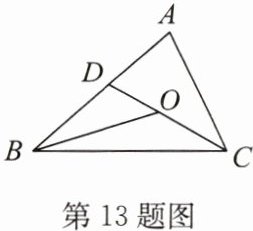
答案:13.证明:在△BOD中,DO+BD>OB,
∴DO+BD+OC>OC+OB,
∴DB+DC>OC+OB.
在△ACD中,AC+AD>CD,
∴AC+AD+BD>CD+BD,
∴AB+AC>CD+BD,
∴AB+AC>OB+OC.