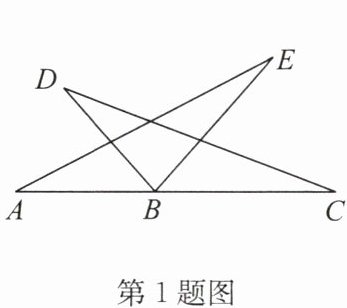
1.(2024·玉环三模)如图,$AB= BD$,$BC= BE$,要使$\triangle ABE\cong \triangle DBC$,需添加条件 (
A
)
A.$AE= DC$
B.$DC= AC$
C.$∠D= ∠E$
D.$AB= BE$
答案:A
解析:
在$\triangle ABE$和$\triangle DBC$中,已知$AB=BD$,$BC=BE$。
若添加条件$AE=DC$,则根据边边边(SSS)全等判定定理,可得$\triangle ABE\cong\triangle DBC$。
A
2.如图,$AB$,$CD$,$EF相交于点O$,且被点$O$平分,$DF= CE$,$BF= AE$,则图中全等三角形的对数为 (
C
)
A.1
B.2
C.3
D.4
答案:C
解析:
∵AB,CD,EF相交于点O,且被点O平分
∴OA=OB,OC=OD,OE=OF
在△AEO和△BFO中
OA=OB,∠AOE=∠BOF,OE=OF
∴△AEO≌△BFO(SAS)
在△DOF和△COE中
OD=OC,∠DOF=∠COE,OF=OE
∴△DOF≌△COE(SAS)
在△AEC和△BFD中
AE=BF,CE=DF,AC=BD(OA+OC=OB+OD)
∴△AEC≌△BFD(SSS)
全等三角形共3对
C
3.如图,$AB= AC$,$BD= DC$,则下列结论不正确的是 (
C
)

A.$∠B= ∠C$
B.$∠ADB= 90^{\circ}$
C.$∠B= 2∠BAD$
D.$AD平分∠BAC$
答案:C
解析:
∵AB=AC,
∴∠B=∠C(A正确)。
∵BD=DC,
∴AD是△ABC中线。
∵AB=AC,
∴AD⊥BC,AD平分∠BAC(B、D正确)。
无法得出∠B=2∠BAD,C不正确。
C
4.如图,点$E$,$F在AC$上,$AD= BC$,$DF= BE$,要使$\triangle ADF\cong \triangle CBE$,只需添加一个条件,则这个条件可以是
AF=CE(答案不唯一)
.
答案:AF=CE(答案不唯一).
5.如图,在$\triangle ABC和\triangle DEF$中,点$B$,$C$,$E$,$F$在同一条直线上,$AB= DE$,$AC= DF$,$BE= CF$,$∠A= 85^{\circ}$,$∠DEF= 25^{\circ}$,则$∠F$的度数为
70°
.
答案:70°
解析:
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l}AB=DE \\AC=DF \\BC=EF\end{array}\right.$
∴△ABC≌△DEF(SSS)。
∴∠B=∠DEF=25°。
在△ABC中,∠A+∠B+∠ACB=180°,∠A=85°,
∴∠ACB=180°-∠A-∠B=180°-85°-25°=70°。
∵△ABC≌△DEF,
∴∠F=∠ACB=70°。
70°
6.(2024·杭州期末)如图,点$A$,$D$,$B$,$E$在同一条直线上,$AC= EF$,$AD= BE$,$BC= DF$. 求证:$∠ABC= ∠EDF$.

答案:证明:
∵AD=BE,
∴AB=DE.在△ACB和△EFD中,$\left\{\begin{array}{l} AC=EF,\\ BC=DF,\\ AB=ED,\end{array}\right. $
∴△ACB≌△EFD(SSS),
∴∠ABC=∠EDF.
7.如图,已知$∠ABC$,以点$B$为圆心,适当长为半径作弧,分别交$AB$,$BC于点P$,$D$;作一条射线$FE$,以点$F$为圆心,$BD长为半径作弧l$,交$EF于点H$;以点$H$为圆心,$PD$长为半径作弧,交弧$l于点Q$;作射线$FQ$. 这样可得$∠QFE= ∠ABC$,其依据是
SSS
.
答案:SSS