7. 如图①,点 B,F,C,E 在同一条直线上,$AB // ED$,$AC // FD$,AD 交 BE 于点 O.
(1)已知______,求证:AD 平分 CF.
请在下列三个条件中,选择一个补充到上面的横线上,并完成解答.
你选择的条件是
①
(填序号)①$AB = DE$;②$AC = DF$;③$BF = EC$.
解:
(1)选择①:
∵AB//ED,AC//FD,
∴∠B=∠E,∠ACB=∠DFE.
∵AB=DE,
∴△ACB≌△DFE(AAS),
∴AC=DF.
∵AC//DF,
∴∠OAC=∠ODF,∠OFD=∠OCA,
∴△OAC≌△ODF(ASA),
∴OF=OC,即AD平分CF.
(2)若将$△DEF$的边 EF 沿 BE 方向移动,使$BF = EC$,如图②,则(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(1)中的结论仍然成立.证明如下:
∵AB//ED,AC//FD,
∴∠B=∠E,∠ACF=∠DFC,
∴180°-∠ACF=180°-∠DFC,即∠ACB=∠DFE.
∵BF=EC,
∴BF-CF=EC-CF,即BC=EF,
∴△ACB≌△DFE(ASA),
∴AC=DF.
∵AC//DF,
∴∠OAC=∠ODF,∠OFD=∠OCA,
∴△OAC≌△ODF(ASA),
∴OC=OF,即AD平分CF.
答案:解:
(1)选择①:
∵AB//ED,AC//FD,
∴∠B=∠E,∠ACB=∠DFE.
∵AB=DE,
∴△ACB≌△DFE(AAS),
∴AC=DF.
∵AC//DF,
∴∠OAC=∠ODF,∠OFD=∠OCA,
∴△OAC≌△ODF(ASA),
∴OF=OC,即AD平分CF.
选择②:
∵AC//FD,
∴∠OAC=∠ODF,∠OCA=∠OFD.
∵AC=DF,
∴△OAC≌△ODF(ASA),
∴OF=OC.即AD平分CF.
选择③:
∵AB//ED,AC//FD,
∴∠B=∠E,∠ACB=∠DFE.
∵BF=EC,
∴BF+CF=EC+CF,即BC=EF,
∴△ACB≌△DFE(ASA),
∴AC=DF.
∵AC//DF,
∴∠OAC=∠ODF,∠OFD=∠OCA,
∴△OAC≌△ODF(ASA),
∴OF=OC,即AD平分CF.
(2)
(1)中的结论仍然成立.证明如下:
∵AB//ED,AC//FD,
∴∠B=∠E,∠ACF=∠DFC,
∴180°-∠ACF=180°-∠DFC,即∠ACB=∠DFE.
∵BF=EC,
∴BF-CF=EC-CF,即BC=EF,
∴△ACB≌△DFE(ASA),
∴AC=DF.
∵AC//DF,
∴∠OAC=∠ODF,∠OFD=∠OCA,
∴△OAC≌△ODF(ASA),
∴OC=OF,即AD平分CF.
8. (1)如图①,在$△ABC$中,点 D,E,F 分别在边 BC,AB,AC 上,$∠B = ∠FDE = ∠C$,$BE = DC$. 求证:$DE = DF$;
(2)如图②,在$△ABC$中,$BA = BC$,$∠B = 45^{\circ}$. 点 D,F 分别是边 BC,AB 上的动点,且$AF = 2BD$. 以 DF 为腰向右侧作等腰$△DEF$,使得$DE = DF$,$∠EDF = 45^{\circ}$. 连接 CE. 探究线段 DC,BD,BF 之间的数量关系,并直接写出$∠ECD$的度数.
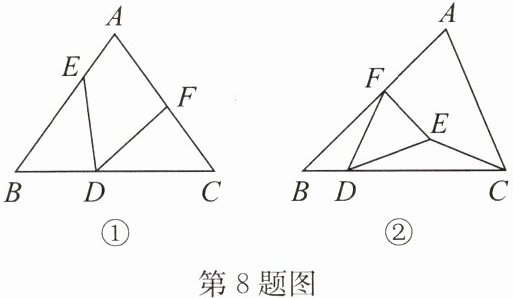
答案:
(1)证明:
∵∠EDF+∠FDC=∠B+∠BED,∠EDF=∠B,
∴∠FDC=∠BED.
在△EBD和△DCF中,∠B=∠C,
BE=CD,
∠BED=∠CDF,
∴△EBD≌△DCF(ASA),
∴DE=DF.
(2)解:
∵AB=BC,
∴AF+BF=BD+DC.
∵AF=2BD,
∴2BD+BF=BD+DC,
∴BD+BF=DC.
在CD上截取DM=BF,连接EM.
∵∠B=45°,∠EDF=45°,
同
(1)可得:∠BFD=∠EDM.
∵DF=DE,
∴△BDF≌△MED(SAS),
∴BD=ME,MD=BF,∠B=∠DME=45°.
∵CD=BD+BF=DM+CM,
∴CM=BD,
∴EM=CM,
∴∠MCE=∠MEC.
∵∠EMD=45°,
∴∠ECD=∠MEC=22.5°.