7. 如图,已知△ABC、△ADE都是等腰直角三角形,连接BD,CE.
(1)求证:△BAD≌△CAE;
(2)若延长BD交CE于点F,试判断BF与CE的位置关系,并说明理由.
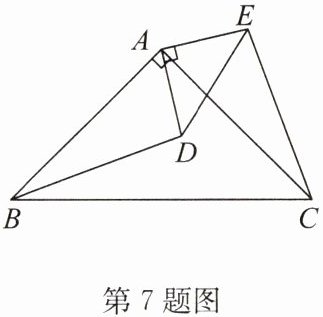
答案:(1)证明:
∵△ABC、△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAC - ∠DAC=∠DAE - ∠DAC,
即∠BAD=∠CAE.
在△BAD和△CAE中,
AB=AC,
{∠BAD=∠CAE,
AD=AE,
∴△BAD≌△CAE(SAS).
(2)解:BF⊥CE.理由如下:如答图.
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∴∠DBC+∠BCF=∠DBC+∠ACB+∠ABD=45° + 45°=90°,
∴∠BFC=90°,
∴BF⊥CE;

8. 如图,在△ABC中,AB= CB,∠ABC= 90°,D为AB的延长线上一点,点E在BC边上,且BE= BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE= 30°,求∠EDC的度数.

答案:
(1)证明:
∵∠ABC=90°,D为AB的延长线上一点,
∴∠ABE=∠CBD=90°.
在△ABE和△CBD中,
AB=CB,
{∠ABE=∠CBD,
BE=BD,
∴△ABE≌△CBD.
(2)解:
∵AB=CB,∠ABC=90°,
∴∠CAB=45°,
又
∵∠CAE=30°,
∴∠BAE=15°.
由
(1)知△ABE≌△CBD,
∴∠BCD=∠BAE=15°,
∴∠BDC=90° - 15°=75°,
又
∵BE=BD,∠DBE=90°,
∴∠BDE=45°,
∴∠EDC=75° - 45°=30°.