6. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着BC的方向平移到$\triangle DEF$的位置,$AB= 10,DO= 4$,平移距离为6,则阴影部分的面积为
48
.
答案:48
解析:
∵两个直角三角形全等,平移距离为6,
∴$S_{\triangle ABC}=S_{\triangle DEF}$,$BE=6$,$DE=AB=10$。
∵$DO=4$,
∴$OE=DE-DO=10-4=6$。
∵$S_{\triangle ABC}-S_{\triangle OEC}=S_{\triangle DEF}-S_{\triangle OEC}$,
∴阴影部分面积$=S_{梯形ABEO}$。
$S_{梯形ABEO}=\frac{1}{2}(AB+OE)\cdot BE=\frac{1}{2}×(10+6)×6=48$。
48
7. 如图,在平面直角坐标系中,$\triangle OAB的顶点坐标分别是A(-6,0),B(0,4),\triangle OA'B'\cong \triangle AOB$,若点$A'$在x轴上,则点$B'$的坐标是
(6,-4)
.
答案:(6,-4)
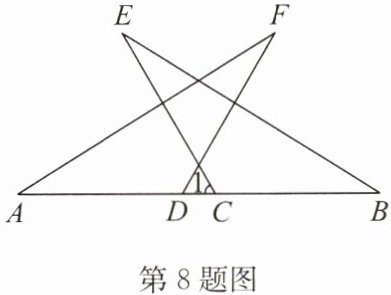
8. 如图,$\triangle ADF\cong \triangle BCE,∠B= 32^{\circ },∠F= 28^{\circ },BC= 5cm,CD= 1cm$.
(1)求$∠1$的度数;
(2)求AC的长.
答案:解:
(1)
∵△ADF≌△BCE,∠F=28°,
∴∠E=∠F=28°.
∵∠B=32°,
∴∠1=∠B+∠E=32°+28°=60°.
(2)
∵△ADF≌△BCE,BC=5 cm,
∴AD=BC=5 cm.
又 CD=1 cm,
∴AC=AD+CD=6 cm.
9. 如图,A,D,E三点在同一条直线上,且$\triangle BAD\cong \triangle ACE$.
(1)求证:$BD= CE+DE$;
(2)当$∠BAC$满足什么条件时,$BD// CE$?并说明理由.

答案:
(1)证明:
∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE.
(2)解:当∠BAC=90°时,BD//CE.理由如下:
∵∠BAC=90°,
∴∠BAE+∠CAE=90°.
∵△BAD≌△ACE,
∴∠ABD=∠CAE,∠ADB=∠AEC,
∴∠ABD+∠BAD=90°,
∴∠ADB=90°,
∴∠BDE=90°,∠AEC=∠ADB=90°,
∴∠BDE=∠AEC,
∴BD//CE.