1. 如图,已知$\triangle CAD\cong \triangle CBE$,若$∠A= 20^{\circ },∠C= 60^{\circ }$,则$∠CEB$的度数为(
C
)
A.$80^{\circ }$
B.$90^{\circ }$
C.$100^{\circ }$
D.$110^{\circ }$
答案:C
解析:
在$\triangle CAD$中,$\angle A=20^{\circ}$,$\angle C=60^{\circ}$,由三角形内角和为$180^{\circ}$得:$\angle ADC=180^{\circ}-\angle A-\angle C=180^{\circ}-20^{\circ}-60^{\circ}=100^{\circ}$。
因为$\triangle CAD\cong\triangle CBE$,所以$\angle CEB=\angle ADC=100^{\circ}$。
C
2. 如图,已知$\triangle ABC\cong \triangle DEF$,点B,E,C,F依次在同一条直线上. 若$BC= 8,CE= 5$,则CF的长为
3
.
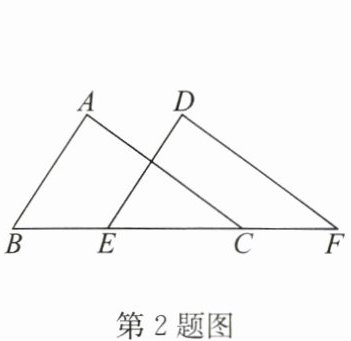
答案:3
解析:
∵△ABC≌△DEF,
∴BC=EF。
∵BC=8,
∴EF=8。
∵点B,E,C,F在同一条直线上,CE=5,
∴CF=EF-CE=8-5=3。
3
3. (2024春·姑苏区月考)如图,$\triangle ABC\cong \triangle ADE$,BC的延长线分别交AD,ED于点F,G,$∠E= 115^{\circ },∠B= 28^{\circ },∠DAC= 50^{\circ }$,则$∠DGF=$
87
$^{\circ }$.

答案:87
解析:
在$\triangle ABC$中,$\angle BAC=180^{\circ}-\angle B-\angle ACB$,
$\triangle ABC\cong\triangle ADE$,$\angle E=115^{\circ}$,$\angle B=28^{\circ}$,
$\angle ACB=\angle E=115^{\circ}$,$\angle BAC=\angle DAE$,$\angle D=\angle B=28^{\circ}$,
$\angle BAC=180^{\circ}-28^{\circ}-115^{\circ}=37^{\circ}$,
$\angle DAE=37^{\circ}$,
$\angle DAC=50^{\circ}$,
$\angle BAF=\angle BAC+\angle DAC=37^{\circ}+50^{\circ}=87^{\circ}$,
在$\triangle ABF$中,$\angle AFB=180^{\circ}-\angle B-\angle BAF=180^{\circ}-28^{\circ}-87^{\circ}=65^{\circ}$,
$\angle DFG=\angle AFB=65^{\circ}$,
在$\triangle DFG$中,$\angle DGF=180^{\circ}-\angle D-\angle DFG=180^{\circ}-28^{\circ}-65^{\circ}=87^{\circ}$。
$87$
4. 如图,已知$\triangle ABF\cong \triangle CDE$.
(1)若$∠B= 30^{\circ },∠DCF= 40^{\circ }$,求$∠EFC$的度数;
(2)若$BD= 10,EF= 2$,求BF的长.

答案:解:
(1)
∵△ABF≌△CDE,∠B=30°,
∴∠D=∠B=30°.
∵∠DCF=40°,
∴∠EFC=∠DCF+∠D=40°+30°=70°.
(2)
∵△ABF≌△CDE,
∴BF=DE,
∴BF-EF=DE-EF,即 BE=DF.
∵BD=10,EF=2,
∴BE=(10-2)÷2=4,
∴BF=BE+EF=6.
5. 有下列说法:①形状相同的两个图形是全等图形;②两个面积相等的正方形是全等形;③全等三角形的面积相等;④若$\triangle ABC\cong \triangle DEF,\triangle DEF\cong \triangle MNP$,则$\triangle ABC\cong \triangle MNP$. 其中正确的有(
D
)
A.0个
B.1个
C.2个
D.3个
答案:D
解析:
①形状相同、大小相等的两个图形是全等图形,原说法错误;
②两个面积相等的正方形边长相等,是全等形,说法正确;
③全等三角形的面积相等,说法正确;
④若$\triangle ABC\cong \triangle DEF$,$\triangle DEF\cong \triangle MNP$,则$\triangle ABC\cong \triangle MNP$,说法正确。
正确的有3个。
D