2025年启东中学作业本八年级数学上册人教版第21页解析答案

9. 如图,$\triangle ABC$ 中,$AD\perp BC$ 于点 $D$,$BE$ 是$\angle ABC$ 的平分线,若$\angle DAC = 30^{\circ}$,$\angle BAC = 80^{\circ}$.
(1) 求$\angle EBC$ 的度数；
(2) 求$\angle AOB$ 的度数.

答案：9.解:
(1)
∵AD⊥BC,
∴∠ADC=90°,
∴△ADC是直角三角形.
∵∠DAC=30°,
∴∠C=90° - ∠DAC=60°.
∵∠BAC=80°,
∴∠ABC=180° - ∠BAC - ∠C=40°.
∵BE是∠ABC的平分线,
∴∠EBC=1/2∠ABC=20°.
(2)
∵∠BAC=80°,∠DAC=30°,
∴∠BAD=∠BAC - ∠DAC=50°.
由
(1)可知∠EBC=20°,
∵BE是∠ABC的平分线,
∴∠ABO=∠EBC=20°,
在△AOB中,∠AOB=180° - ∠BAO - ∠ABO=110°.

10. (2024 春·泰兴期末)如图,$\triangle ABC$ 的顶点在正方形网格的格点上,请按要求画图并回答问题：
(1) 请画图,找出$\triangle ABC$ 的重心点 $P$；
(2) 请在$\triangle ABC$ 的边上找一点 $D$,使它与点 $A$,$B$,$C$ 中的任意两点组成的三角形的面积是$\triangle ABC$ 面积的$\frac{1}{2}$.

答案：
10.解:
(1)如答图①，点P即为所求.

(2)如答图②,找到AB,BC的中点F,E,连接AE,CF交于点P,连接BP,延长BP交AC于点D.
依题意,在△ABC的边上找一点D,使它与点A,B,C中的任意两点组成的三角形的面积是△ABC面积的$\frac{1}{2}$,则点D,E,F均满足题意.

11. 如图,$CE$ 平分$\angle ACD$,$F$ 为 $CA$ 的延长线上一点,$FG// CE$ 交 $AB$ 于点 $G$,$\angle ACD = 100^{\circ}$,$\angle AGF = 20^{\circ}$,求$\angle B$ 的度数.

答案：11.解:
∵CE平分∠ACD,
∴∠ACE=$\frac{1}{2}$∠ACD=$\frac{1}{2}$×100°=50°.
∵FG//CE,
∴∠AFG=∠ACE=50°.
在△AFG中,∠BAC=∠AFG+∠AGF=50°+20°=70°,
又∠ACB=180° - ∠ACD=180° - 100°=80°,
∴∠B=180° - ∠BAC - ∠ACB=180° - 70° - 80°=30°.

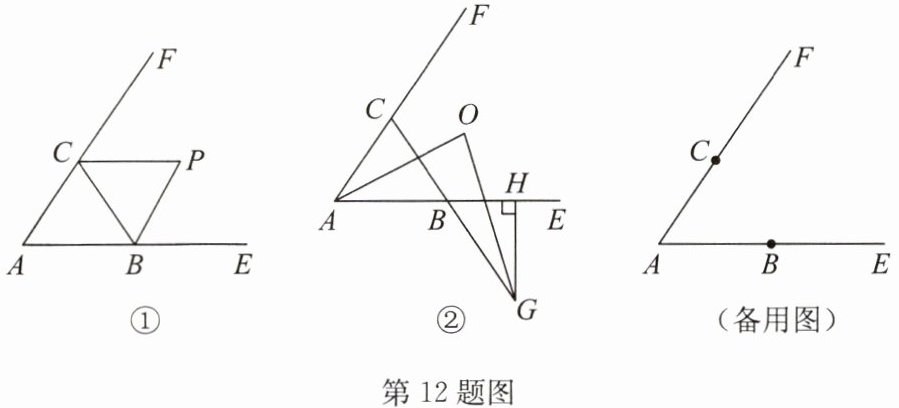
12. 如图,已知锐角$\angle EAF$,点 $B$,$C$ 分别在射线 $AE$,$AF$ 上.
(1) 如图①,若$\angle EAF = 56^{\circ}$,连接 $BC$,$\angle ABC = \alpha$,$\angle ACB = \beta$,$\angle CBE$ 的平分线与$\angle BCF$ 的平分线交于点 $P$,则$\alpha+\beta=$______$^{\circ}$,$\angle P= $______$^{\circ}$；
(2) 若点 $Q$ 在$\angle EAF$ 的内部(点 $Q$ 不在线段 $BC$ 上),连接 $BQ$,$QC$,$\angle EAF = 56^{\circ}$,$\angle CQB = 104^{\circ}$,$BM$,$CN$ 分别平分$\angle QBE$ 和$\angle QCF$,且 $BM$ 与 $CN$ 交于点 $D$,求$\angle BDC$ 的度数；
(3) 如图②,$G$ 是线段 $CB$ 的延长线上一点,过点 $G$ 作 $GH\perp AE$ 于点 $H$,$\angle EAF$ 与$\angle CGH$ 的平分线交于点 $O$,请直接写出$\angle ACG$ 与$\angle AOG$ 的数量关系,并说明理由.

答案：
12.
(1)124 62
(2)解:①当点Q在BC的右侧时,如答图①.

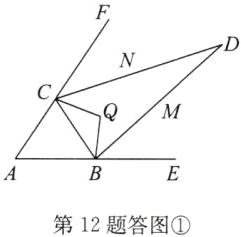
∵∠ACQ+∠ABQ=360° - (∠EAF+∠CQB)=360° - (56°+104°)=200°,
∴∠FCQ+∠QBE=360° - (∠ACQ+∠ABQ)=160°.
∵BM,CN分别平分∠QBE,∠QCF,
∴∠DCQ+∠QBD=$\frac{1}{2}$(∠FCQ+∠QBE)=80°.
∵∠QCB+∠CBQ=180° - ∠CQB=76°,
∴∠DCB+∠DBC=80°+76°=156°,
∴∠BDC=180° - (∠DCB+∠DBC)=180° - 156°=24°.
②当点Q在BC的左侧时,如答图②.

∵∠ACB+∠ABC=180° - ∠EAF=124°,
∴∠ACQ+∠ABQ=124° - 76°=48°,
∴∠FCQ+∠QBE=360° - 48°=312°,
∴∠DCQ+∠QBD=$\frac{1}{2}$(∠FCQ+∠QBE)=156°,
∴∠BDC=360° - 156° - 104°=100°.
综上所述,∠BDC的度数为24°或100°.
(3)解:∠AOG - $\frac{1}{2}$∠ACG=45°.理由如下:如答图③.

∵AO,GO分别是∠FAE和∠CGH的平分线,
∴∠CAO=$\frac{1}{2}$∠EAF,∠CGO=$\frac{1}{2}$∠CGH.
∵∠1=∠CAO+∠ACG=∠CGO+∠AOG,
∴$\frac{1}{2}$∠EAF+∠ACG=$\frac{1}{2}$∠CGH+∠AOG,
即∠AOG - ∠ACG=$\frac{1}{2}$(∠EAF - ∠CGH).
∵∠ABC=∠GBH,
∴∠EAF=180° - ∠ACG - ∠ABC=180° - ∠ACG - ∠GBH,∠CGH=90° - ∠GBH,
∴∠AOG - ∠ACG=$\frac{1}{2}$(90° - ∠ACG),
∴∠AOG - $\frac{1}{2}$∠ACG=45°.